データの整理
度数分布表
階級:データの値の範囲を区切った区間。
階級の幅:階級としての区間の幅。
階級値:階級の真ん中の値。
度数:各階級に入るデータの個数。
度数分布表:各階級に度数を対応させた表。
相対度数分布表
相対度数:各階級の度数の全体に対する割合。
累積度数:各階級に対し、度数を最初の階級からその階級の値まで合計したもの。
累積相対度数:相対度数についての累積度数
ヒストグラム
度数分布表に整理された資料を柱状のグラフで表したもの。
データの整理の例題
(例題①)
次のデータは、ある月の
(単位は
(1) 階級の幅を
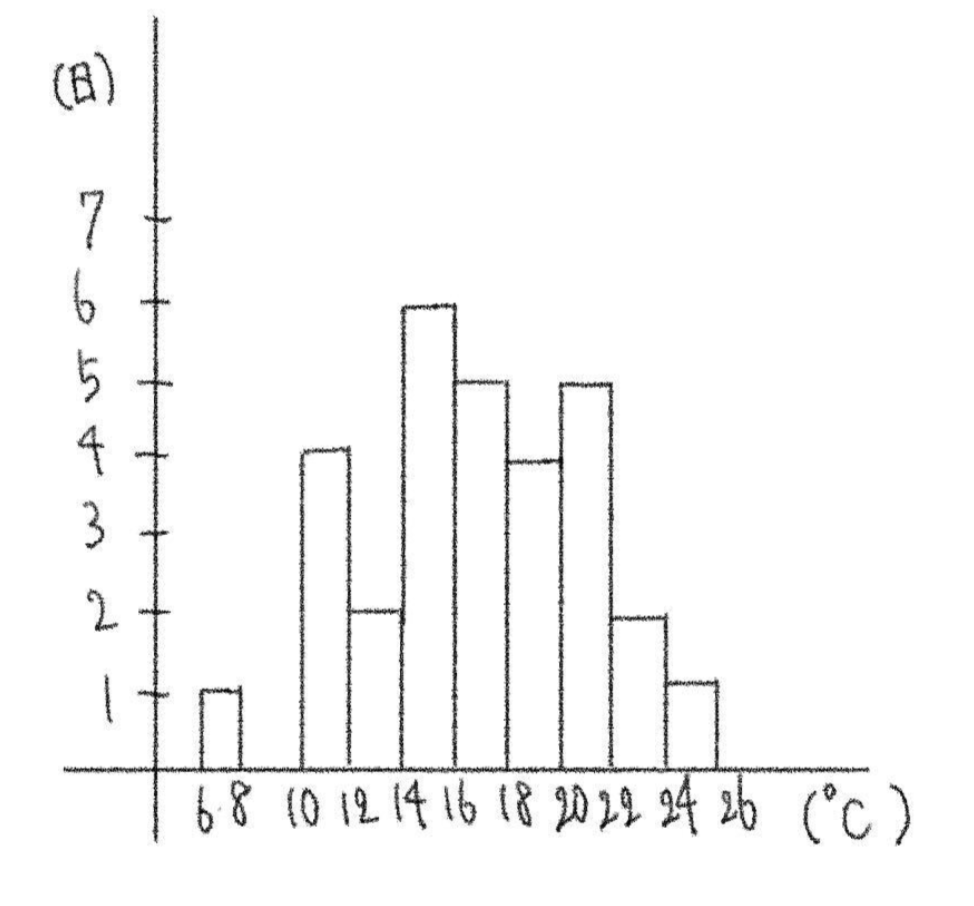
(2) (1) で作った度数分布表をもとにして、ヒストグラムをかけ。
解説
(1) 階級の区切り始めと階級の幅から、各階級に入るデータの数を数え、表にする。
| 階級 | 度数 |
| 1 | |
| 0 | |
| 4 | |
| 2 | |
| 6 | |
| 5 | |
| 4 | |
| 5 | |
| 2 | |
| 1 | |
| 計 | 30 |
(2) (1) の度数分布表をもとに、柱状のグラフにして表す。ヒストグラムの各長方形の高さは、各階級の度数を表す。
(例題②)
次のデータは、
(単位は点)
(1)
(2)
解説
(1)
よって、約
(2)
データの代表値
平均値
大きさ
中央値(メジアン)
データを値の大き沙の順に並べたとき、中央の位置にくる値。
最頻値(モード)
データが度数分布表に整理されているときは、度数が最も大きい階級の階級値を最頻値とする。
データの代表値の例題
(例題)
次のデータは、
(1) 平均値を求めよ
(2) 中央値を求めよ
(3) 最頻値を求めよ
(1)
(2)
データを大きい順に並べると、
データの大きさが奇数より中央値は
(3)
データを大きい順に並べると、
よって、最頻値は
>>詳細はこちらから
データの散らばりと四分位範囲
範囲
データの最大値と最小値の差。
四分位数
データを大きさの順に並べたとき、
四分位数範囲、四分位偏差
四分位範囲:
四分位偏差:
箱ひげ図
データの最小値、第
データの散らばりと四分位範囲の例題
(例題)
次のデータは、
(1) データの範囲を求めよ。
(2) データの第
(3) データの四分位範囲、四分位偏差を求めよ。
データを大きい順に並び替えると
(1)
よって、
(2)
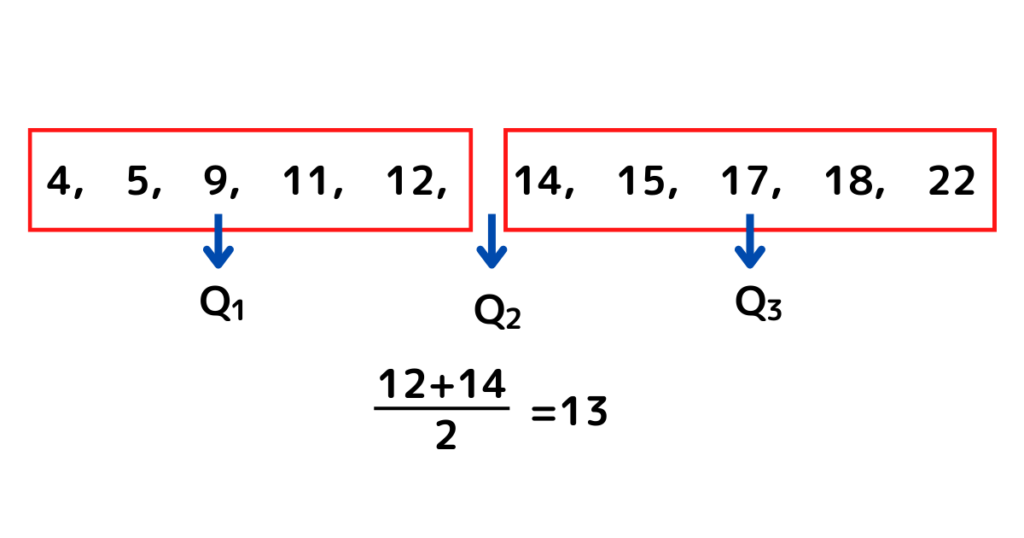
第
第
第
(3)
四分位範囲:
四分位偏差:
おわりに
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。



