代表値
統計学における代表値は、データセット全体を簡潔に要約するための指標であり、データの中心的な傾向や分布の特徴を示します。
代表値の中でも特に重要なのは、平均値(Mean)、中央値(Median)、最頻値(Mode)の3つです。それぞれの定義、関係性、そして例題を含めて解説します。
平均値 (Mean)
平均値は、データセット内の全ての値の合計をデータの個数で割った値です。全体の傾向を最もよく表す指標の一つであり、データが全体としてどの程度の大きさかを示します。
ここで、
例:データセットが
特徴:平均値はデータの全体的な傾向を反映しますが、極端に大きい値や小さい値(外れ値)によって影響を受けやすいという欠点があります。
中央値 (Median)
中央値は、データセットを昇順または降順に並べたとき、中央に位置する値です。データの個数が偶数の場合、中央の2つの値の平均を取ります。
データを昇順に並べた後、データ数が奇数の場合は中央の値、偶数の場合は中央の2つの値の平均を取ります。
例:データセットが
もしデータセットが
特徴:中央値は外れ値の影響を受けにくく、特に非対称な分布や極端な外れ値を含むデータセットの場合に有用です。
最頻値 (Mode)
最頻値は、データセット内で最も頻繁に現れる値です。同じ値が複数回出現する場合にその値が最頻値となります。
例:データセットが
データセットが
特徴:最頻値はデータセットの中で最も一般的な値を示しますが、データが均等に分散している場合、最頻値が存在しないか、複数の最頻値が存在することもあります。
代表値の関係性と適用例
代表値の関係性
平均値、中央値、最頻値は、データセットの分布に応じて異なる情報を提供します。
例えば、正規分布の場合、これらの値は近似的に一致します。下の図のように正規分布は左右対象に分布しているため
平均値 = 中央値 = 最頻値となります。
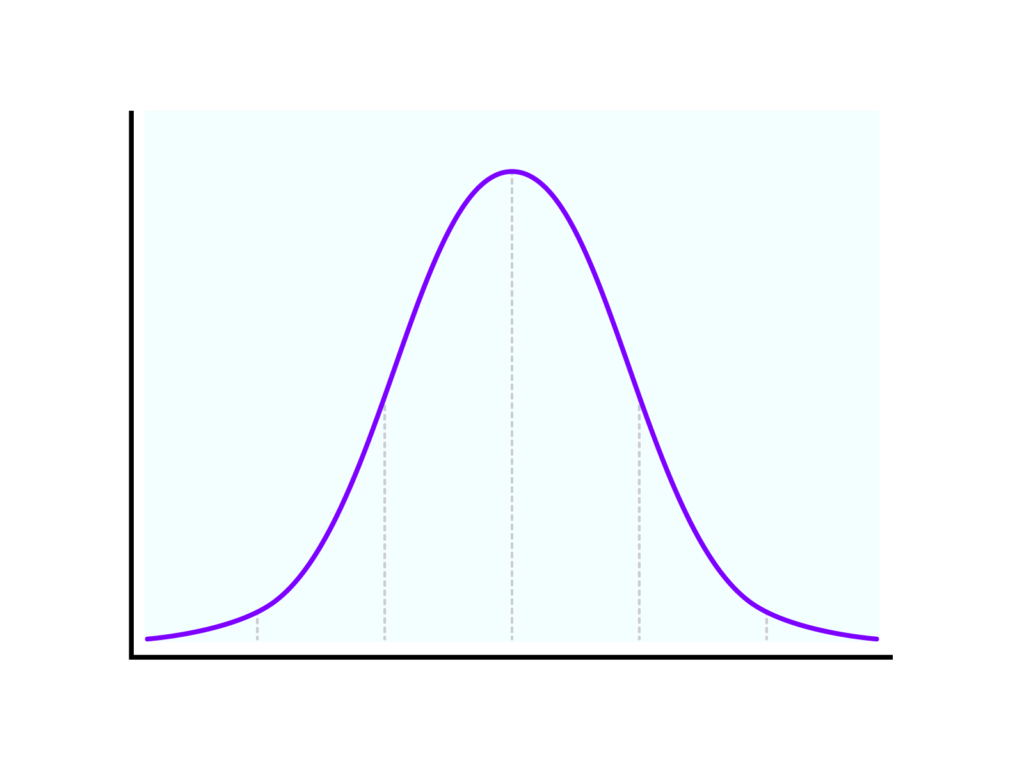
一方で、データが偏っている(歪んでいる)場合、これらの値は大きく異なることがあります。
・右に歪んだ分布: 最頻値 < 中央値 < 平均値
・左に歪んだ分布: 平均値 < 中央値 < 最頻値
適用例:
・平均値は一般的にデータ全体の傾向を知りたいときに有用ですが、外れ値の影響を受けやすいです。
・中央値は住宅価格や所得分布のように、極端な値が存在するデータセットに対して有効です。
・最頻値はカテゴリー型データ(例: 投票結果、人気商品)に対して適用され、どのカテゴリーが最も一般的かを示すために使用されます。
まとめ
代表値は、データセットの全体像を把握するための重要な指標です。
平均値はデータの中心的傾向を示し、中央値はデータの中間点を表し、最頻値は最もよく現れる値を示します。
これらの指標はデータの特性に応じて使い分けることで、より正確なデータ分析が可能となります。
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。


