\(y=\sin\theta\) のグラフ
\(y\) の範囲：\(-1\leq y\leq 1\)
周期：\(2\pi\)
\(y=\cos\theta\) のグラフ
\(y\) の範囲：\(-1\leq y\leq 1\)
周期：\(2\pi\)
\(y=\tan\theta\) のグラフ
周期：\(\pi\)
三角関数のグラフの特徴と描き方
グラフを学ぶ 2 ステップ
① 値を入れてみる。
\(\theta=0\), \(\frac{\pi}{4}\), \(\frac{\pi}{2}\), \(\pi\), \(\frac{3}{2}\pi\), \(2\pi\) を順番に代入し \(y\) の値を求める。
② グラフの概形を覚える。
実際に問題を解く際は、①のように値を代入していては時間が足りないのである程度形の理解が進んだら概形を覚えてしまいましょう！
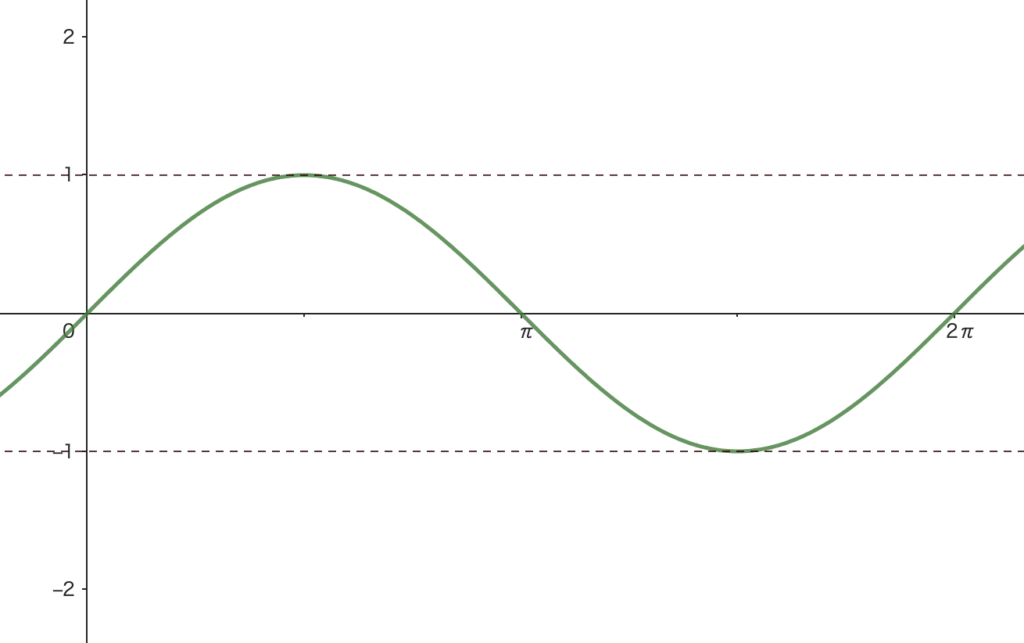
\(y=\sin\theta\) のグラフ
\(y\) の値の範囲：\(-1\leq y\leq 1\), 周期：\(2\pi\)
以下の点をグラフ上に打って点をつなげてグラフを描いてみよう！
\(\theta=0\) のとき \(y=0\)
\(\theta=\frac{\pi}{4}\) のとき \(y=\frac{1}{\sqrt{2}}\)
\(\theta=\frac{\pi}{2}\) のとき \(y=1\)
\(\theta=\pi\) のとき \(y=0\)
\(\theta=\frac{3}{2}\pi\) のとき \(y=-1\)
\(\theta=2\pi\) のとき \(y=0\)
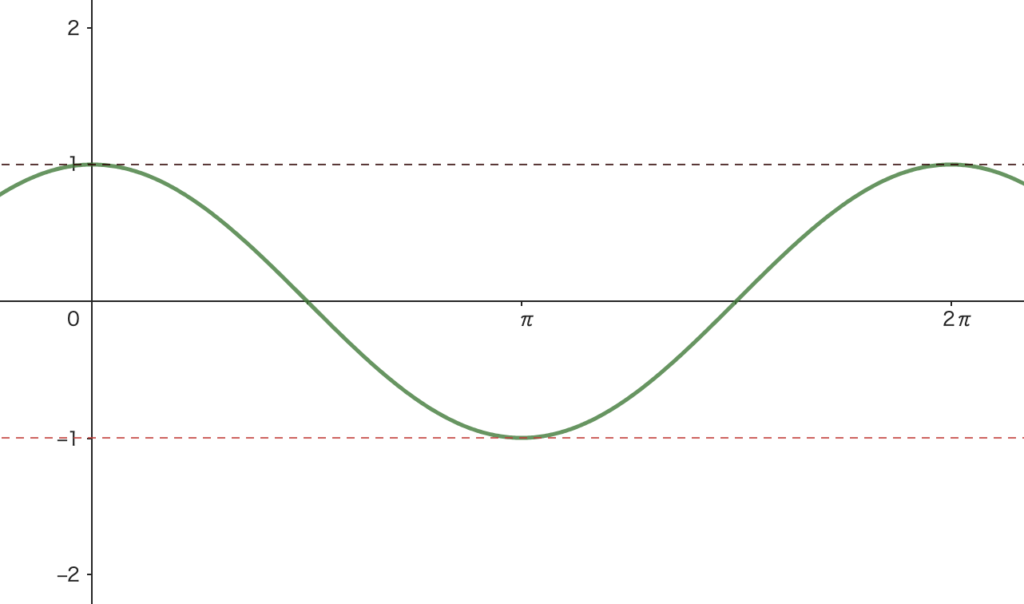
\(y=\cos\theta\) のグラフ
\(y\) の範囲：\(-1\leq y\leq 1\), 周期：\(2\pi\)
以下の点をグラフ上に打って点をつなげてグラフを描いてみよう！
\(\theta=0\) のとき \(y=1\)
\(\theta=\frac{\pi}{4}\) のとき \(y=\frac{1}{\sqrt{2}}\)
\(\theta=\frac{\pi}{2}\) のとき \(y=0\)
\(\theta=\pi\) のとき \(y=-1\)
\(\theta=\frac{3}{2}\pi\) のとき \(y=0\)
\(\theta=2\pi\) のとき \(y=1\)
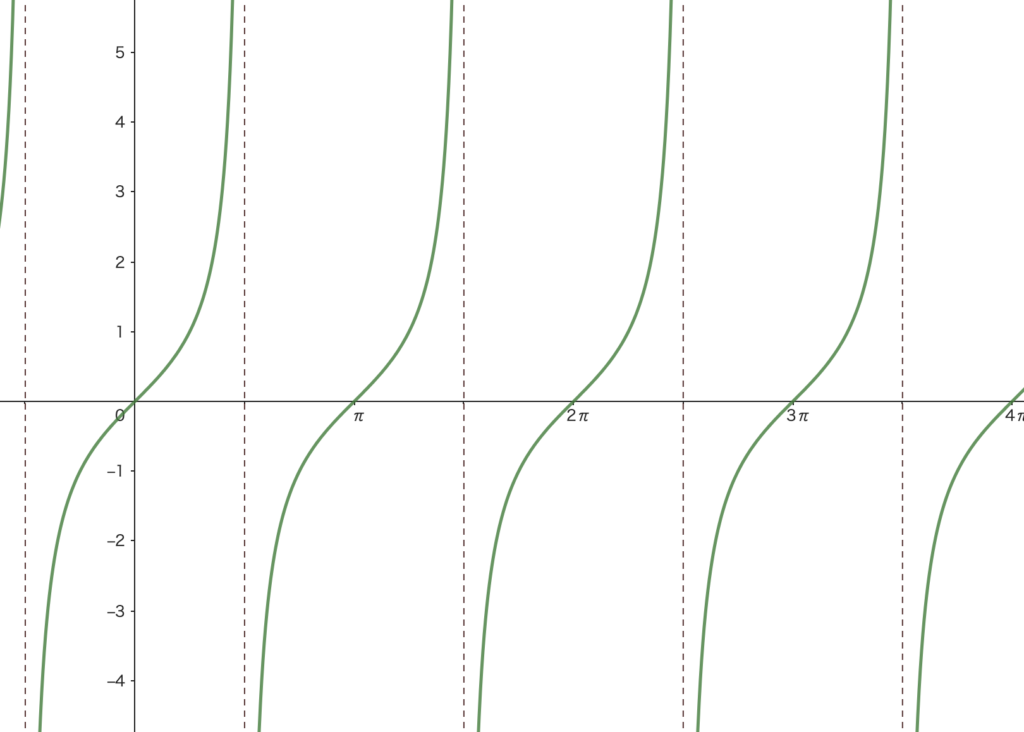
\(y=\tan\theta\) のグラフ
周期：\(\pi\)
以下の点をグラフ上に打って点をつなげてグラフを描いてみよう！
\(\theta=0\) のとき \(y=0\)
\(\theta=\frac{\pi}{4}\) のとき \(y=1\)
\(\theta=\frac{\pi}{2}\) のとき値なし
\(\theta=\pi\) のとき \(y=0\)
\(\theta=\frac{3}{2}\pi\) のとき値なし
\(\theta=2\pi\) のとき \(y=0\)
理系大学レベル別おすすめ数学テキスト
＞＞【理系大学向け】レベル別おすすめの数学参考書
三角関数のグラフの応用
\(\sin\theta\) のグラフがどう変化するのかを意識しながら見ていってください！
※ \(\cos\theta\) のグラフも同様に考えることができます。
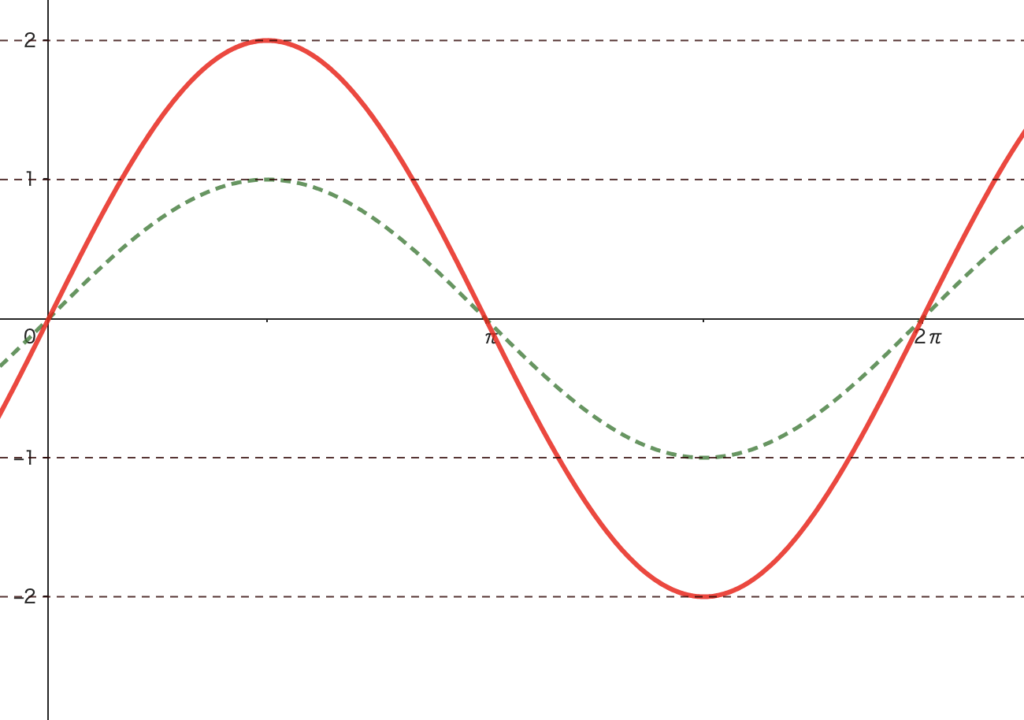
\(y=2\sin\theta\) のグラフ
変更点：\(-1\leq \theta\leq 1\) \(\longrightarrow\) \(-2\leq \theta\leq 2\)
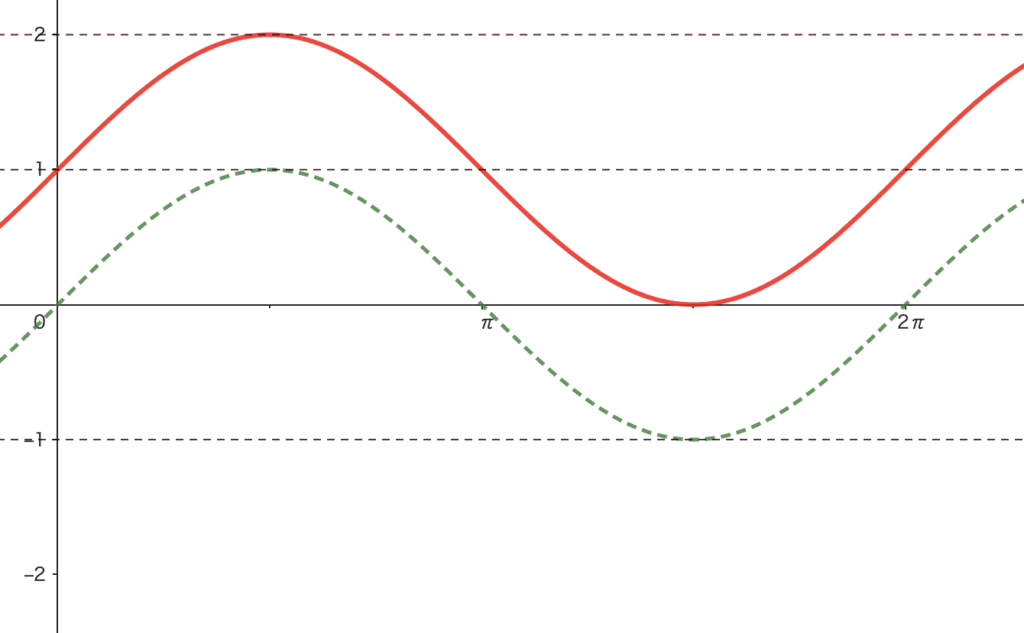
\(y=\sin\theta+1\) のグラフ
変更点：\(-1\leq \theta\leq 1\) \(\longrightarrow\) \(0\leq \theta\leq 2\)
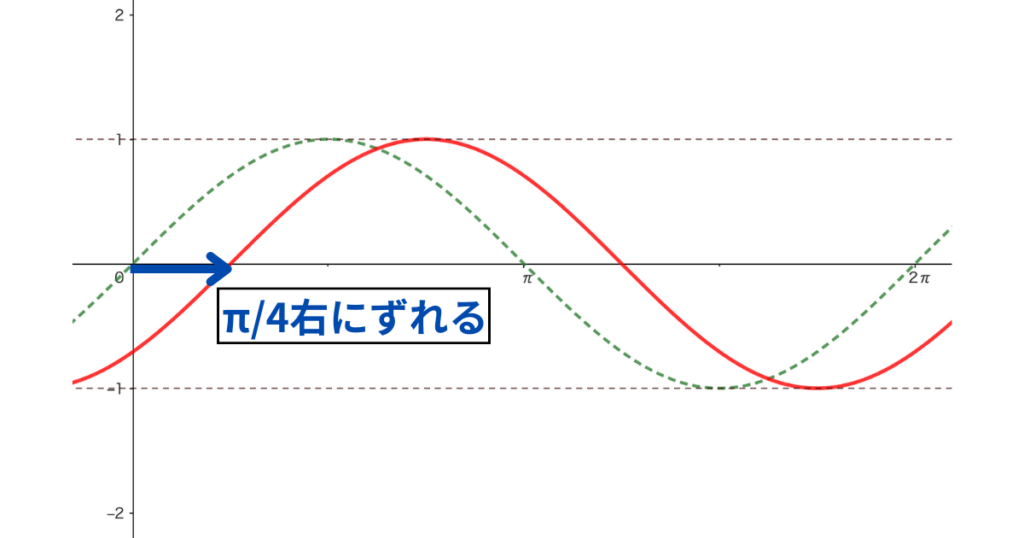
\(y=\sin(\theta-\frac{\pi}{4})\) のグラフ
変更点：右に\(\frac{\pi}{4}\) ずれる。
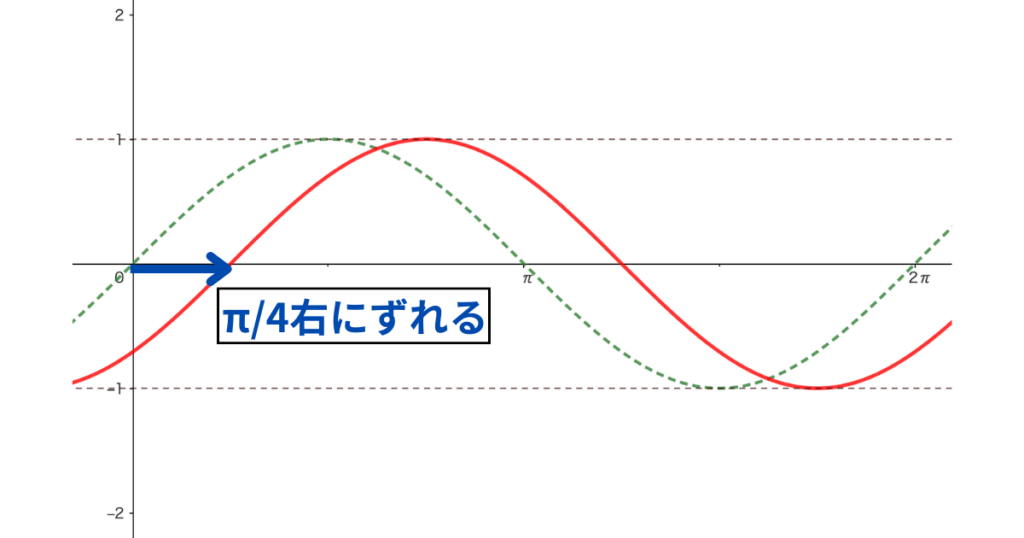
\(\sin(\theta-\frac{\pi}{4})\) って、マイナスなのに、右にずれるの？
y=\(\sin\theta\) と y=\(\sin(\theta-\frac{\pi}{4})\) それぞれが \(y=0\) になるときの \(\theta\) がいくつになるかを考えればいいよ！
\(0=\sin\theta\) のとき \(\theta=0\)
\(0=\sin(\theta-\frac{\pi}{4})\) のとき \(\theta=\frac{\pi}{4}\) となるので、グラフは \(\theta=\frac{\pi}{4}\) からスタートする。
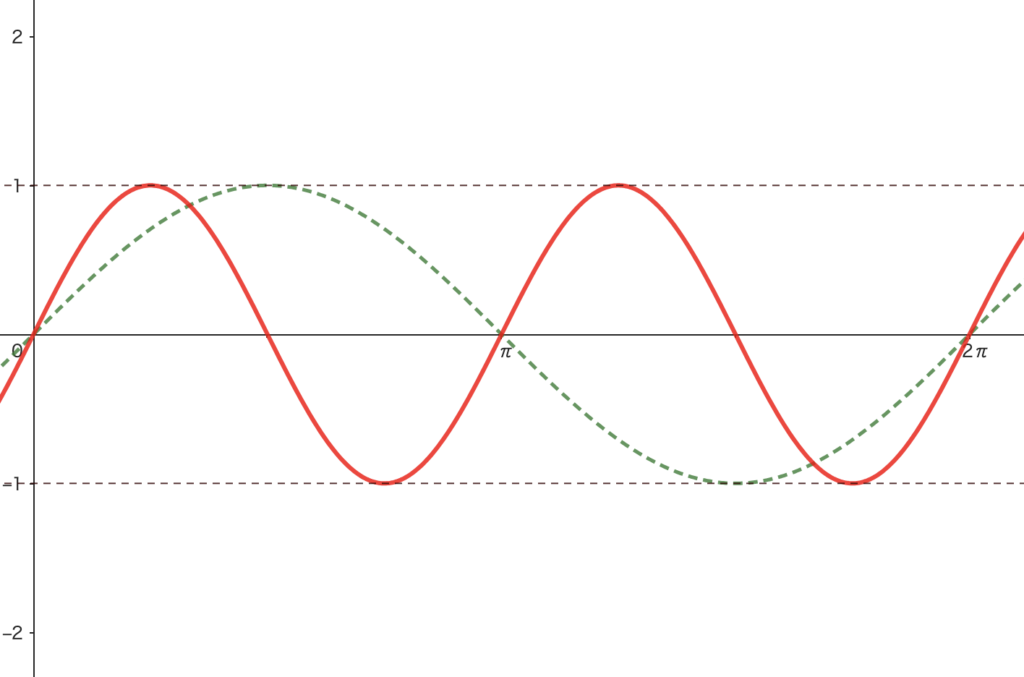
\(y=\sin2\theta\) のグラフ
変更点：周期 \(2\pi\) \(\longrightarrow\) \(\pi\)
三角関数のグラフの例題
（問題）
関数 \(2\sin\big(\displaystyle\frac{\theta}{2}-\frac{\pi}{4}\big)\) のグラフをかけ。またその周期を求めよ。
（解説）
STEP ① \(y=\sin\big(\displaystyle\frac{\theta}{2}\big)\) のグラフを描く
周期が \(2\) 倍
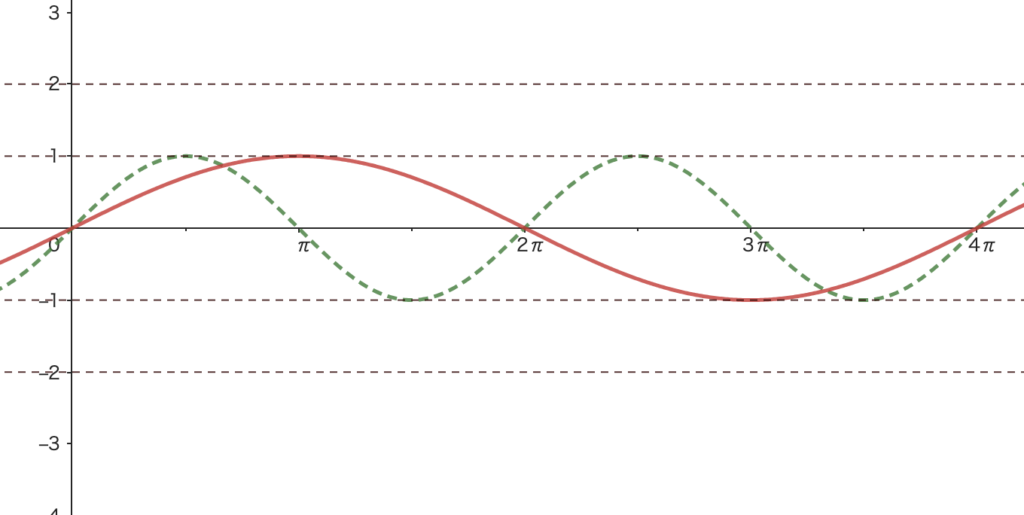
STEP ② \(y=2\sin\big(\displaystyle\frac{\theta}{2}\big)\) のグラフを描く
\(y\) 軸方向に \(2\) 倍
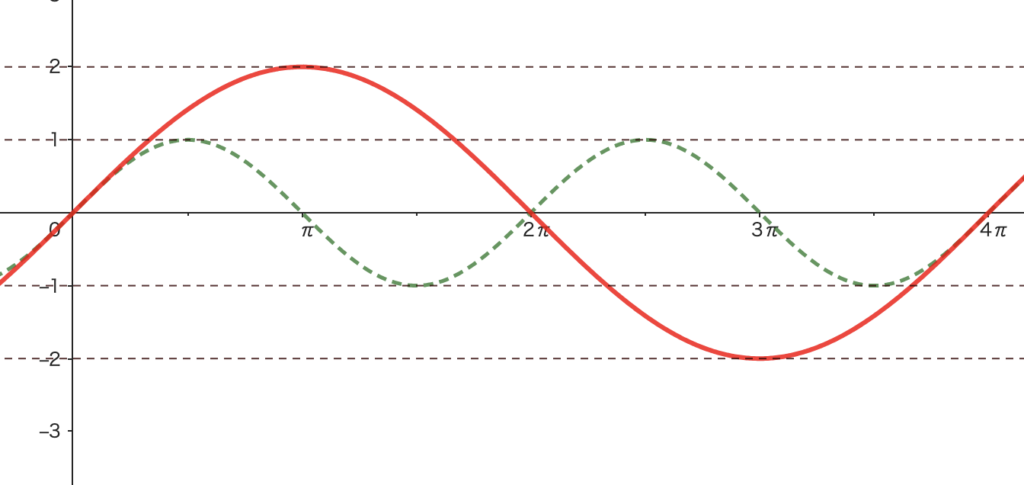
STEP ② \(y=2\sin\big(\displaystyle\frac{\theta}{2}-\frac{\pi}{4}\big)\) のグラフを描く
おわりに
さいごまで記事を読んでいただきありがとうございました！
「30分で集中力が切れてしまう方へ」
勉強の集中力UPのために
子供に集中して宿題をさせるために
会議やプレゼンのタイムマネジメントのために
ポチップ
質問や感想はコメントへ！