グラフの概形をイメージせよ！
今回は、変域が変化する場合の問題を扱っていきます。
元の式に文字が \(2\) 種類含まれている場合の最大・最小の問題は以前に扱っていますが、今回は変域が変化します。
変域が動けば、その範囲内での最大・最小が変化するのは当然ですね。
どの範囲ならばグラフがどんな形をしているのか、そのときのグラフの概形をイメージすることが、このタイプの問題を解くコツです。
では、見ていきましょう。
最大値と最小値（問題）
関数 \(f(x)=x^2-5x+3(0 \leq x \leq a)\) の最大値と最小値を求めなさい。
最大値と最小値（答案の例）
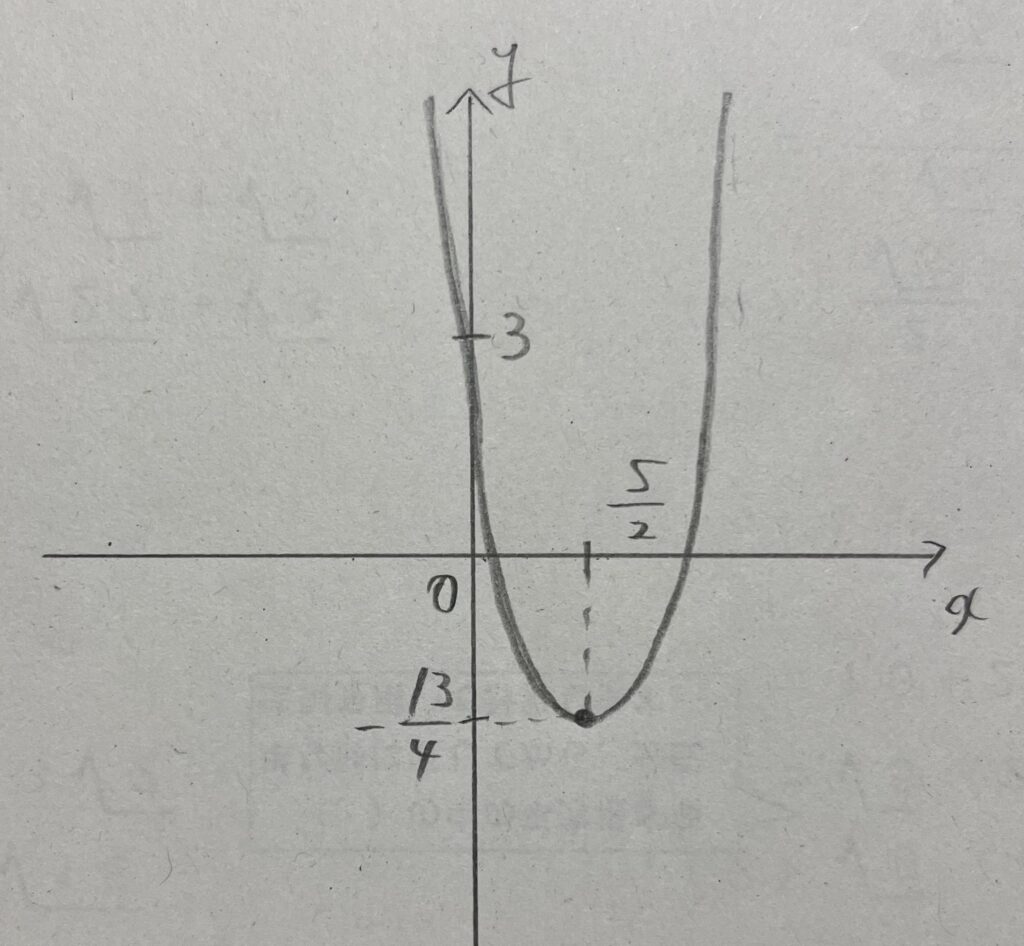
\(f(x)=(x- \dfrac{5}{2})^2- \dfrac{13}{4}\) なので、以下のようなグラフになる。
① \(0 < a <\dfrac{5}{2}\) のとき
最大値は、
\(f(0)=3\)
最小値は、
\(f(a)=a^2-5a+3\)
② \(\dfrac{5}{2} \leq a \leq 5\) のとき
最大値は、
\(f(0)=3\)
最小値は、
\(f(\dfrac{5}{2})=- \dfrac{13}{4}\)
③ \(5 < a\) のとき
最大値は、
\(f(a)=a^2-5a+3\)
最小値は、
\(f(\dfrac{5}{2})=- \dfrac{13}{4}\)
最大値と最小値（解説）
最大値と最小値の \(2\) つについて聞かれているため、分けて考えましょう。
最大値に着目した場合、どこが分岐点になるのでしょうか？
\(x=0\) スタートは変わらないので、そこから下にグラフが下がっていくため、しばらくは最大値は \(x=0\) のときの \(y\) の値（ \(f(0)\) の値）ということになります。（図 \(1\) ）
このときの値は、
\(f(0)=3\)
となります。
最大値が切り替わるタイミングは、グラフが再び上がり始めて、\(f(0)=3\)と同じになった時ですね。
これ以降グラフが上がっていくと、最大値はどんどん大きくなっていくことになります。（図 \(2\) ）
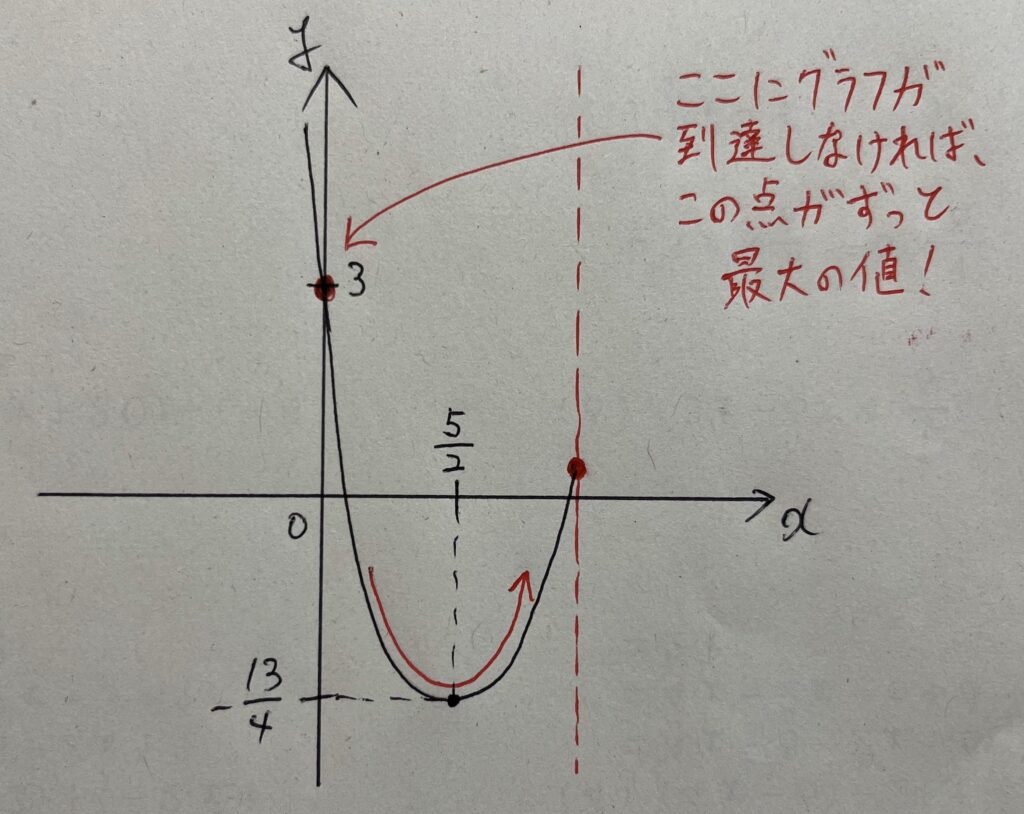
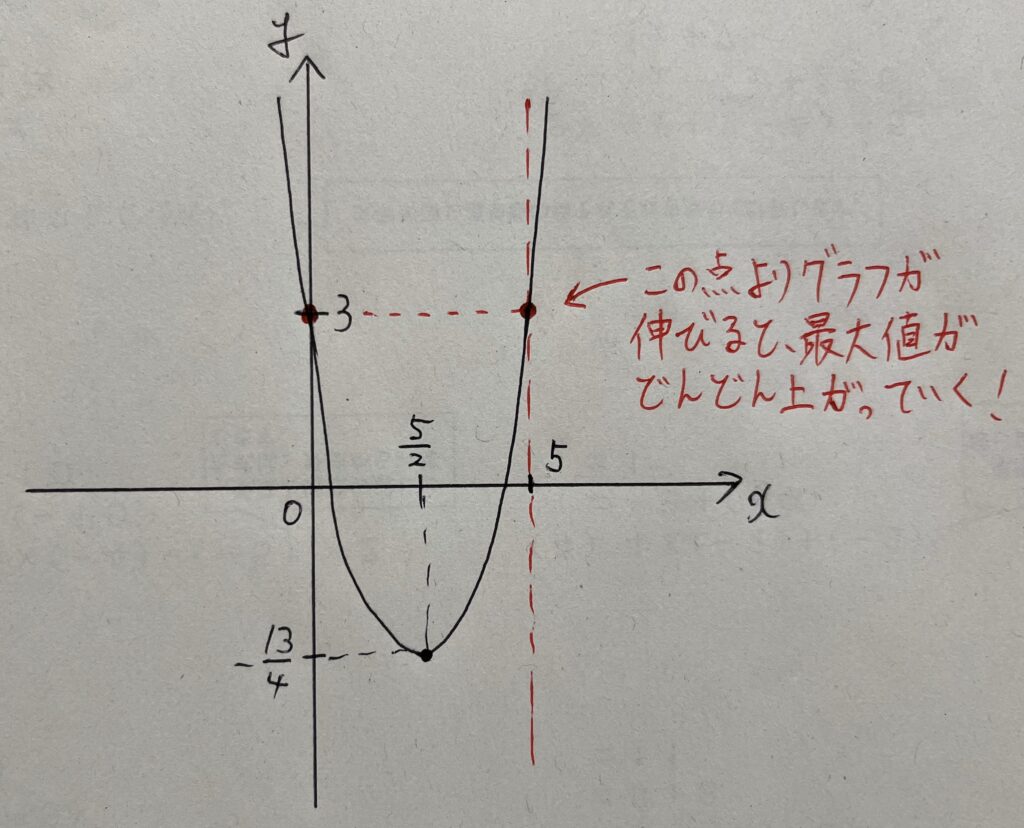
そして最大値が切り替わるときの \(x\) の値は、 \(y\) の値が \(3\) になるときのもう一つの \(x\) の値なので、
\(3=x^2-5x+3\)
\(x^2-5x=0\)
\(x(x-5)=0\)
よって、 \(x=0,5\)。これにより、もう一つの \(x\) の値は \(5\) であることがわかります。（図 \(2\) ）
つまり、最大値は「 \(0\) から \(5\) まで」「 \(5\) 以上」という \(2\) つの区間で区分されることになります。
次に最小値ですが、こちらは頂点を経由するかどうかで決まります。（図 \(3\) ）
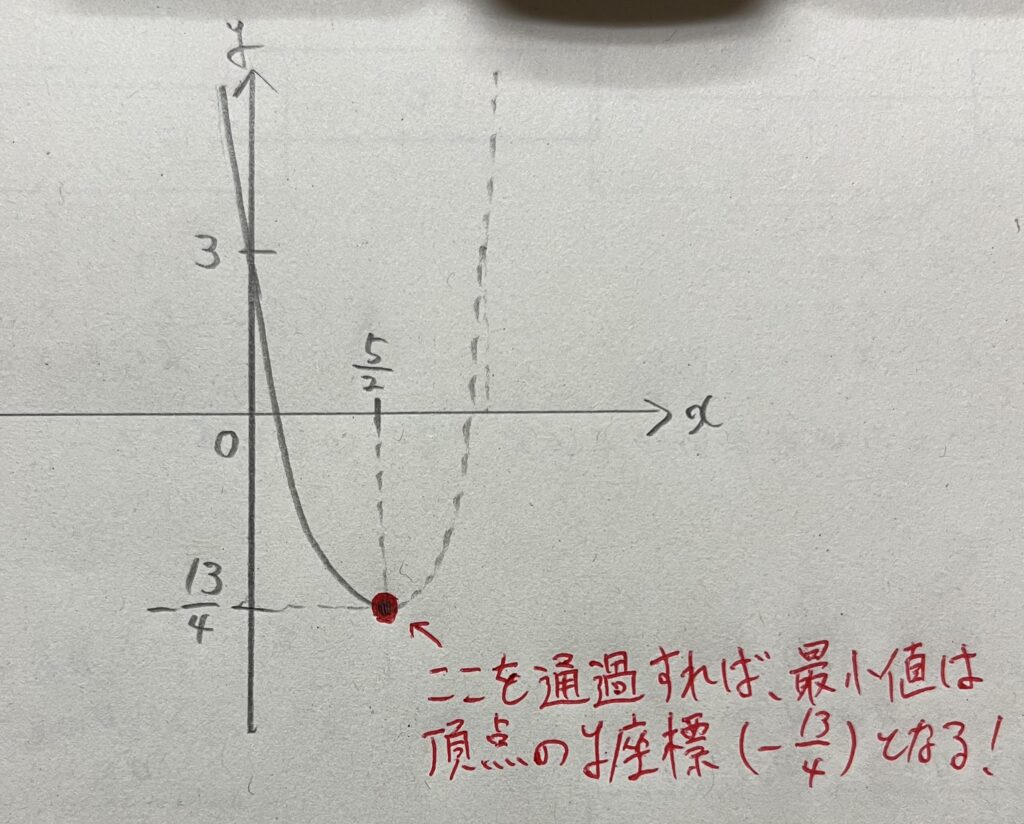
図 \(3\) のように、頂点を通過すれば、以降頂点の \(y\) 座標を下回るものは出てこないため、頂点が最小値の切り替わる点ということになります。
よって、「 \(0\) から \(\dfrac{5}{2}\) まで」「\(\dfrac{5}{2}\) 以上」という \(2\) つの区間で区分されます。
これまでのことを整理すると、図 \(4\) のような分け方をすれば、最大と最小の変化をうまくカバーできることになります。
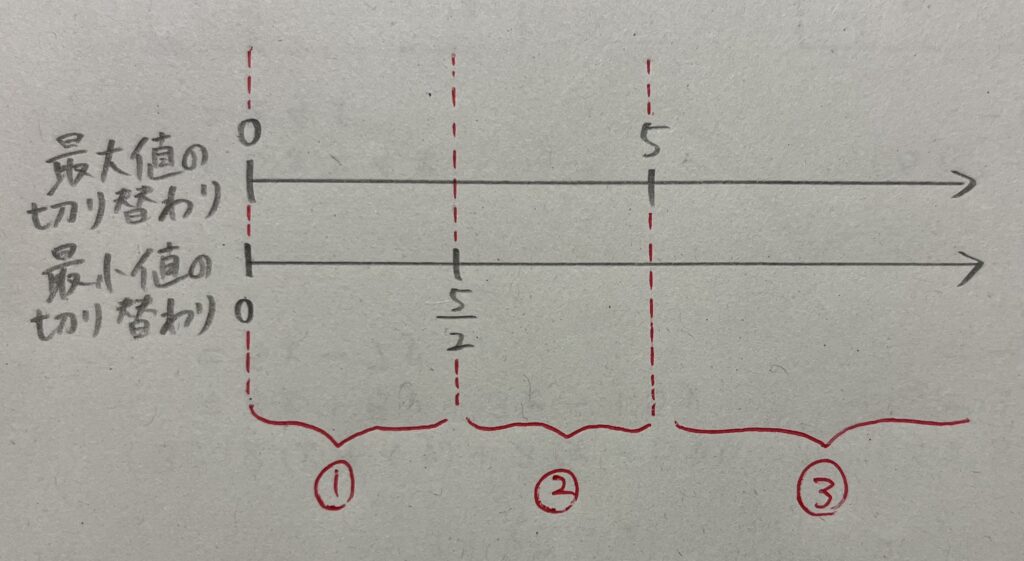
つまり、
\(0 < a <\) \(\dfrac{5}{2}\) のとき
\(\dfrac{5}{2} \leq a \leq 5\) のとき
\(5\) \( < a\) のとき
の \(3\) 種類です。
ちなみに、最大値や最小値が \(a\) の値で変化する部分は「＜（小なり）」となっています。
すなわち、上記の範囲の赤の部分ですね。