命題のコツ（判断推理）
数的処理には、判断推理・数的推理・資料解釈の3分野があります（ただし、判断推理に含まれる図形問題を別途「空間把握」として、4分野と説明する場合もあります）。
数的処理は、公務員として必要な事務処理能力を問うものです。
その中でも「判断推理」は、パズルクイズのような問題をイメージするとよいでしょう。
命題、論理、暗号、対応関係、順序、嘘つき問題など、問題文に書かれてある複数の条件を整理し推測する問題が出題されます。
論理力が要求される問題が多いのが特徴です。また、立体図形や展開図・図形を転がすなど空間認識能力が問われる問題（「空間把握」といいます）があるのも特徴的なところです。
立体図形の見えない底面や裏面を推理したり、切り取られた立体図形の切断面の形状を考えたり、圧倒的に多くの受験生が苦手とする分野です。直感で解くには限界がありますが、空間把握独特のノウハウさえマスターすれば、短時間で解けるようになります。
出題分野は以下のとおりです。（分類の仕方は諸説あります）
論理/真偽/対応関係/試合/順序関係/位置関係/数量推理/暗号/操作手順/推理
判断推理の対策～解法パターンを確立しよう～
数的処理を苦手とする受験生は多いのですが、それでも数的推理のようにストレートに数的処理学の知識が必要とされないせいか、判断推理は数的推理に比べて苦手意識は低いようです。
では、判断推理はどのような戦略で取り組むべきでしょうか？
まず、出題数から見てみましょう。
主な職種の「判断推理」の出題数です（※2019年の本試験データに基づくものです）
国家一般職 8問（空間把握2問）
国家専門職（国税・財務・労基） 8問（空間把握1問）
東京都 7問（空間把握4問）
東京特別区 8問（空間把握4問）
裁判所事務官⼀般職 10問（空間把握3問）
地方上級 自治体によっても異なるが概ね9問（空間把握4〜5問）
市役所 自治体によっても異なるが概ね7問（空間把握3〜4問）
「判断推理」の出題数は、「数的推理」と同程度で、どちらかに極端に偏ることはないのが一般的な傾向ですが、職種による違いはあります。
判断推理に含まれる空間把握の出題数には職種による違いがあるので、結果的に、いわゆる純粋な判断推理の出題数に違いが出てきます。
判断推理の出題分野については、前述しましたが、基本的な考え方のバリエーションはわずかです。
しかも、判断推理の平均的な難易度は決して高くはありません。
このように判断推理は、得点源になる分野といえます。
ですが、判断推理には思わぬ落とし穴があることに注意が必要です。
確かに、とっつきやすく、数的処理に苦手意識のある受験生にも比較的勉強しやすい分野です。
しかし、きちんと解法パターンを確立しておかないと、「解けるけど時間がかかる」ことになる恐れが多分にあります。
つまり、やってみるとなんとなく解けるからといって、漫然と過去問を解いていると、解法パターンが確立されず、本試験で思わぬ時間の浪費をしてしまう危険性があるということです。
そうならないためにも、解き方を暗記するだけでなく、どの手順で解答にたどりつくか、自分なりの解法パターンを確立することが重要ポイントになります。
判断推理の問題例と解き方のコツ
ここでは、限られた時間内で判断推理を確実に解答するためのコツを、実際に本試験で出題された問題を使って解説いたしましょう。
みなさんも、実際に解いてみてください。
制限時間は1問あたり3分です。
判断推理 問題と解説①
ある事件の犯人として、Ａ～Ｅの5人の容疑者が取調べを受け、次のように供述した。
Ａ：「私は犯人ではない」
Ｂ：「Ｄが犯人だ」
Ｃ：「Ｂこそ犯人だ」
Ｄ：「Ａの言っていることは本当だ」
Ｅ：「Ｂは嘘をついている」
ところが、5人のうち1人だけが嘘をついていることが後でわかった。犯人は5人のうちだれか。ただし、犯人は1人だけであるとする。
答え
犯人は B です。
本問のポイントは、「1人だけが嘘をついている」「犯人は1人だけ」です。
基本的な解き方は、AからEまで一人ひとり、嘘をついていると仮定して矛盾がないパターンを探すというやり方です。
※しかしこれだと時間がかかりすぎるのでより工夫したやり方が必要な場合があります。
例えば、Aが嘘を付いてるいるとすると、
A：「私は犯人である。」
となり、BからEは真実を言っていることになります。よって、
B：「Dが犯人である。」
と矛盾することになるので、Aは嘘をついていないということになります。
しかし、これだとあまりにも時間がかかりすぎるため、今回の場合は以下のような考え方が最適だと言えます。
条件（1人だけ嘘をついている/犯人は1人）より、B・Cのどちらか1人が嘘つきであることがわかります。なぜなら、BもCも正直者だとすると、犯人がD・Bの2人になってしまい、「犯人は1人だけ」と矛盾するからです。
すると、Eは正直者になります（嘘をついているのは1人だけで、それはB・Cのどちらかだからです）。Eの発言から、B・Cのうち、Bが嘘つきで、Cが正直者となり、Cの発言から犯人はBとわかります。
この問題は、「真偽」という頻出分野からの出題です。基本となる考え方は「論理」で学ぶ、論理力です。
ここでは、
①条件（犯人は1人、嘘つきは1人）に着目する
②矛盾する発言（BもCも正直者だとすると矛盾します）に着目する。
以上の2つのテクニックを使い、集中して思考すれば、1分もかからずに答えが出せます。
もちろん、色んな解き方がありますが、最短で解答できる解き方を覚えるべきなのです。
判断推理 問題と解説②
Ａ～Ｄの４人が円いテーブルを囲んで歓談をしている。４人はそれぞれ国籍が異なり（アメリカ・イギリス・フランス・ドイツ）、それぞれ異なる色（青・赤・黒・白）の帽子をかぶっている。次のことがわかっているとき、確実にいえることとして妥当なのはどれか。
ア Ａの右側の人は黒の帽子をかぶっており、左側の人はフランス人である。
イ Ｂの右側の人はイギリス人であり、左側の人は赤の帽子をかぶっている。
ウ Ｃの右側の人はアメリカ人であり、左側の人は青の帽子をかぶっている。
エ Ｄの右側の人は白の帽子をかぶっており、左側の人はドイツ人である。
１ Ａは赤い帽子をかぶっている。
２ Ｂはフランス人である。
３ Ｃはドイツ人である。
４ ドイツ人は黒の帽子をかぶっている。
５ イギリス人は白の帽子をかぶっている。
答え
4
こちらも先程の問題と同様、時間はかかりますが1〜5を仮定しながら考えれば解くことができます。
例えば、選択肢1が正しいと仮定して図を描きます。
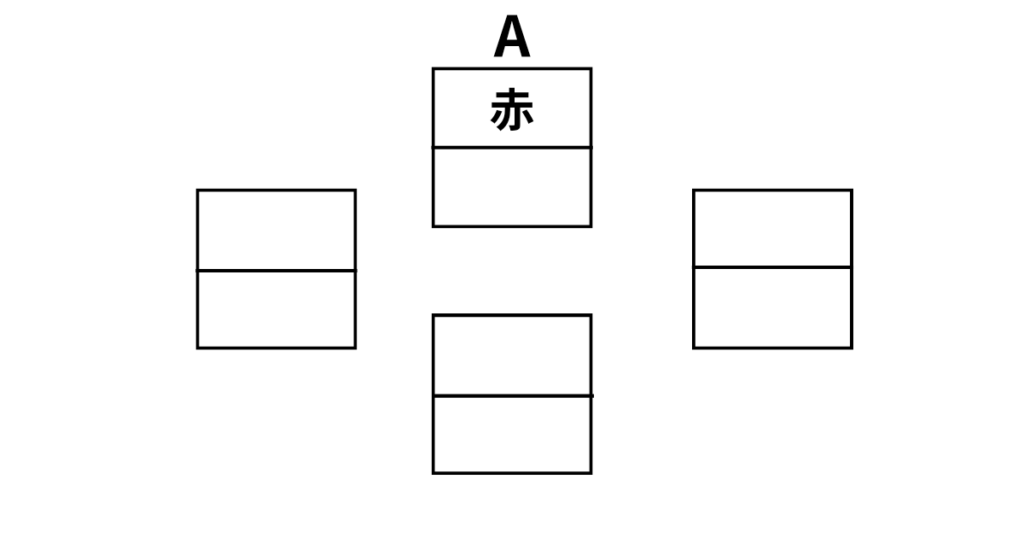
これを基準にアから順番に図に反映させていきます。
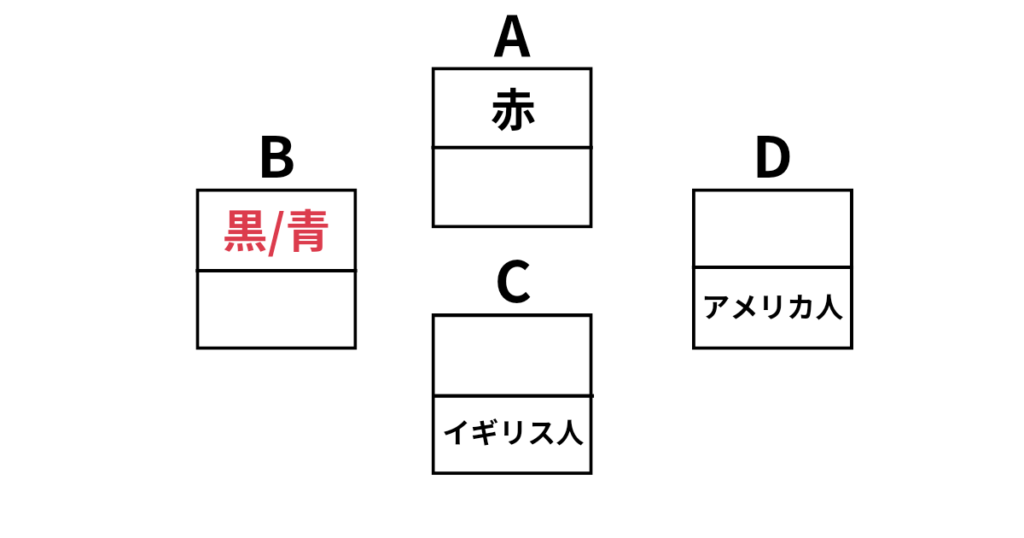
そうすると、アとウで赤字の部分が重複してしまい、選択肢1は誤りであることがわかります。このように一つ一つ仮定していくと解けますが、時間がかかってしまいます。なので、こちらの問題も少し工夫することが大切です。
まずア、イ、ウ、より、Ａの正面には、Ｂでも、Ｃでもありません。
なぜなら、Aの左側がフランス人なので、Aの正面がBだとイの条件（Bの右側がイギリス人）を満たさないし、同様に、Aの正面がCだとウの条件（Cの左側が青の帽子）を満たさないからです。
すると、Aの正面はDなのがわかります。そして、エより、黒の帽子はドイツ人、フランス人は白の帽子なのがわかります。
問題文の条件だけからは、B、Cのいずれがフランス人なのか、ドイツ人なのかはわかりません。
以上から、「確実にいえる」こととして妥当なのは、
４ ドイツ人は黒の帽子をかぶっている。
になります。
本問では条件を図式化すると、条件を整理しやすくなりましたね。
頭の中であれこれ考えるだけでなく、どんどん手を動かすのもテクニックとして重要です。
そして、判断推理には、最後まできっちりと定まらないまま（いくつかの選択肢を残したまま）選択肢を選ばなければならない問題が多々あります。問題文に「確実に言えること」と書かれてあったら、こういうパターンだと予想していいでしょう。
にも関わらず、A〜D全員の帽子の色・国籍が決まるまで延々と考え続けていると、時間オーバーになってしまいます。
数的処理では、問題に対する正確な答えを出すことは目的ではありません。
正解肢を選ぶことが目的であることを忘れないようにしましょう。
判断推理の勉強法
本試験では1問あたりの平均時間は3〜4分です。
このような短時間で解答にたどり着くためには、
ことが必須です。そのためには、知識と反復練習が欠かせません。
暗記すべき解法テクニックは、数的推理に比べて非常に少なくてすみます。
例えば、論理、真偽、対応関係、試合、順序関係、位置関係、数量推理は、出題形式こそ異なりますが、基本となる考え方はほぼ同じです。
論理的な思考力をベースに、下記の3点だけです。
・問題文の読解
・情報の整理
・試行錯誤
ただ、問題に合わせて自分でアレンジすることや解答に至るまでの作業が、数的推理よりも要求されます。
なので、先ずは解法テクニックを知ってください。
先ほど例としてあげた過去問も、市販の過去問集だと違う解き方が掲載されていると思います。ですが、解説を見るたびに、この解き方、あの解き方と右往左往するのではなく、「この種の問題は、このパターンで解く」という自分なりの解法パターンを確立すべきです。
例えば、「対応」の分野で、3つ以上の項目を対応させる問題の場合、3つを対応させる表を作って考えるのか、それとも、あくまで1対1で対応させる表で考えるのか、自分の基本方針を決定させるのです。そのために、何回も過去問を解いて検証するのです。
繰り返しますが、判断推理で暗記すべき知識はわずかです。少ない知識をどうアレンジさせるか（解法パターン）を、反復練習によって確立し、自分のものとするのです。
「前にやった問題はできるけど、初見の問題は解き方が思いつかない。時間内に解けない」
こうおっしゃる方は、知識不足（きちんと暗記していない）か、反復練習が足りないだけです。
勉強が進んでくると思うようになるのが、「判断推理を解くのは面倒くさい」です。
そのとおりです。面倒くさいことをさせるのが判断推理なのです。なぜなら事務処理能力を問う試験だからです。
最後に、本試験ではメモ用紙は配ってくれないことを追記しておきます。
本試験では、問題文の余白に表や図を書かなければなりません。ですから、最初から神経質になる必要はありませんが、本試験間近になってきたら、あまりおおらかにメモ用紙を使わず、コンパクトに整理するように心がけましょうね。
「判断推理に限らず、数的処理はセンスだから生まれつきの能力で左右される。」
そんな風に考えてはいませんでしたか。でも、センスは磨くものであって、生まれつきのものではありません。
おわりに
さいごまで読んでいただきありがとうございました！
【最新】こちらの記事がおすすめ！