判断推理の対偶
逆・裏・対偶
【命題の基本構造】（仮定）ならば（結論）
逆・裏・対偶は、元の命題の形を変更させたものである。
例）
元の命題：りんごであるならば、果物である。
逆 ：果物であるならば、りんごである。
裏 ：りんごでないならば、果物ではない。
対偶 ：果物でないならば、りんごではない。
元の命題 → 逆への変形
（ならば）の両側を交換する。
元の命題 → 裏への変形
（ならば）の両側を否定する。
否定の例）「である。」 → 「ではない。」
元の命題 → 対偶への変形
↓命題についての基本知識はこちら
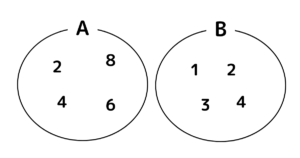
集合の表し方
集合の表し方
(1) 要素を書き並べて表す。
(2) 要素の満たす条件を述べて表す。
例えば、\(1\) 桁の正の偶数の集合 \(A\) は、
(1) では、
\(A=\{2\), \(4\), \(6\), \(8\}\)
(2) では、
\(B=\{x\) | \(n\) は整数, \(1\leq n\leq 4\}\) など
↓集合についての基本知識はこちら
＞＞詳細はこちらから
判断推理の対偶（問題）
今年、大学を受験する人にどの学部を希望しているかアンケートを行ったところ、ア〜ウのことがわかった。
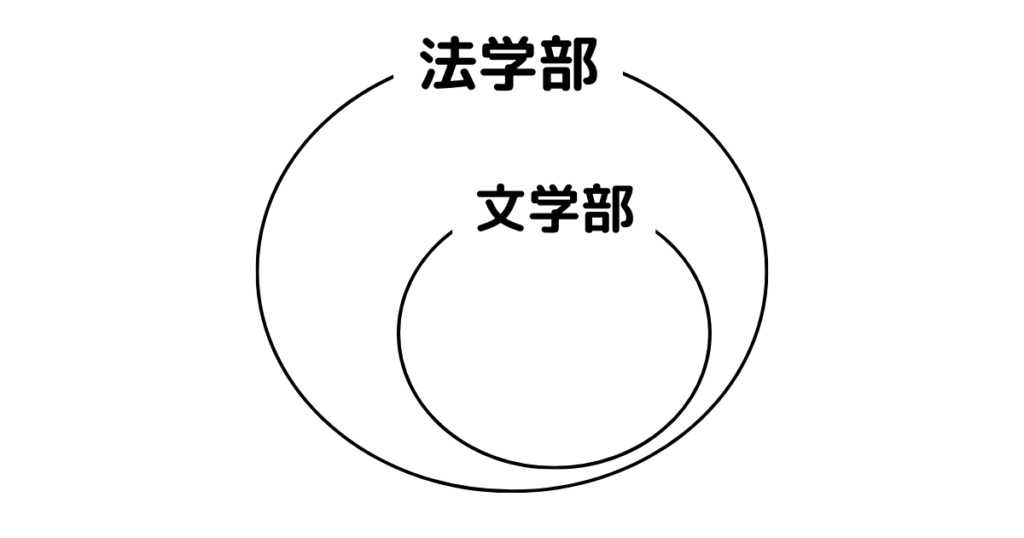
ア：文学部を選んだ人は全員、法学部も選んでいた。
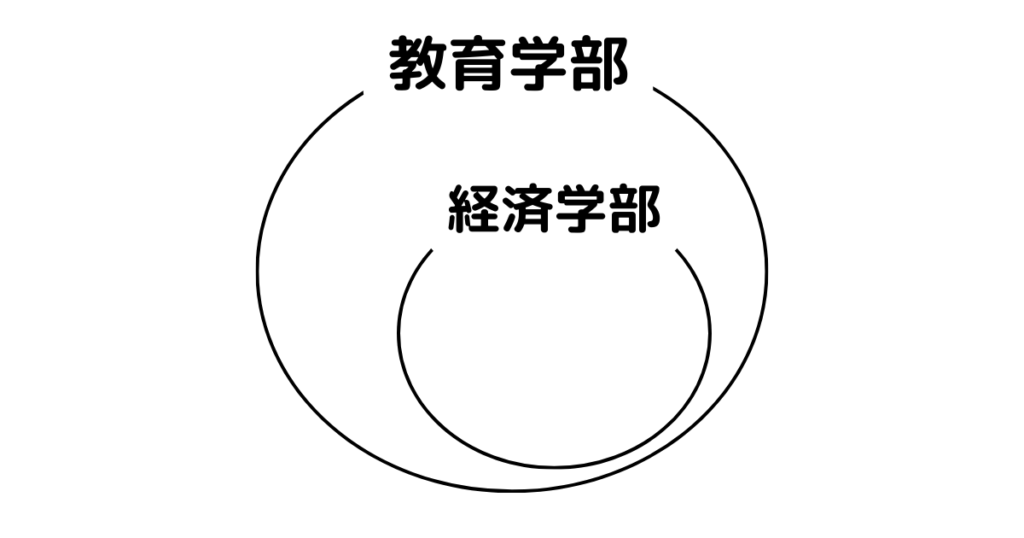
イ：経済学部を選んだ人は全員、教育学部を選んでいた。
ウ：法学部を選んでいない人は全員、教育学部も選んでいない。
このとき、確実にいえるものはどれか。
1 文学部を選んだ人は全員、教育学部も選んでいた。
2 法学部を選んだ人は全員、文学部も選んでいた。
3 経済学部を選んだ人は全員、法学部も選んでいた。
4 教育学部を選んでいない人は全員、法学部を選んでいない。
5 文学部を選んだ人は全員、経済学部を選んでいた。
（解説）
選択肢ア〜ウを見たとき、アイとウが文章構造が異なるのに気づけます。
ア、イは「〜を選んだ人は全員、〜も選んでいた。」になっているのに対して、ウは「〜を選んでいない人は全員、〜も選んでいない。」になっています。
ウの構造に、”対偶”を使ってみます。そうすると、
元の命題「法学部を選んでいない人は全員、教育学部も選んでいない。」
裏 「法学部を選んだ人は全員、教育学部も選んでいた。」
逆 「教育学部を選んで人は全員、法学部も選んでいた。」
対偶にした上で、ア〜ウの選択肢改めて並べてみる。
ア：文学部を選んだ人は全員、法学部も選んでいた。
イ：経済学部を選んだ人は全員、教育学部を選んでいた。
ウ：教育学部を選んで人は全員、法学部を選んでいた。
そうすると、イとウがうまい具合に繋がるのがわかります。
さて、ここまでが与えられた選択肢を見てできることです。ここからは問いの選択肢を見ていきましょう。
そうすると、選択肢 \(3\) 番が正解になることがわかります。
ちなみに他の選択肢について簡単に言っておくと、
1 文学部を選んだ人についての言及はアのみのため確実に正しいとは言えない。
2 アの逆になっているが、命題の特性として逆は必ずしも成り立つとは言えない。
「東京に住んでいるならば、日本に住んでいる。」の逆「日本に住んでいるならば東京に住んでいる。」が必ずしも成り立たないのと同じですね！
4 2と同様でウの逆になっているが必ずしも成り立つとは言えない。
5 1と同様で文学部を選んだ人の元凶はアのみのため確実に正しいとは言えない。
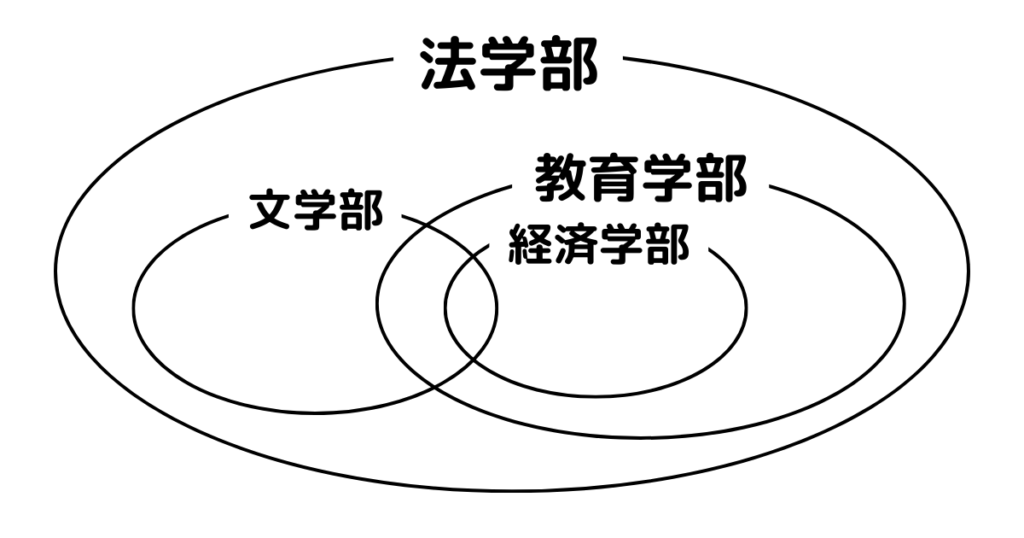
また、ア〜ウの条件をベン図にまとめると以下のようになります。図からも答えを得ることもできます！
おわりに
さいごまで読んでいただきありがとうございました！
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学（統計検定2級レベル）
ぜひご覧ください！
数学でお困りの方は、コメントやXでご連絡ください。（Xはこちら）
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。