【公務員試験対策】『数的推理』旅人算　速さの計算　速さの和と差

旅人算とは、速さの和や差を使って考える計算です！

「旅人算」には、「出会い」「追い越し」という言葉がよく登場します。そして、これらの言葉のせいで多くの中学受験生が混乱してしまいます…混乱しやすいポイントを解説をしながら例題を紐解いていきます。

旅人算（公務員試験対策）

今回は、旅人算の代表的な2パターンである「出会い算」と「追い越し算」について、じっくり考えてみましょう。

旅人算の例題

---

(1)も(2)も、「次郎君は B 地点に向かう途中で、先に B 地点を折り返してきた太郎君に出会いました。」という点では同じです。しかし、「どちらも出会い算だから、速さの和を使おう」と考えると間違いです。

間違うのは、次のような思い込みがあるせいです。

多くの受験生は、「出会う」という言葉を見た瞬間、「速さの和を使う」と考えてしまいます。しかし、実際は、(1)が速さの和を使う問題で、(2)が速さの差を使う問題です。

速さの和を使う問題と速さの差を使う問題では、何が違うのでしょうか？

速さの和を使う問題と差を使う問題を区別するために、道のりに注目する必要があります。

(1)と(2)のそれぞれについて、状況図（線分図）を描いて、$2$ 人の進んだ道のりを見てみましょう。

旅人算の例題(1)の解説

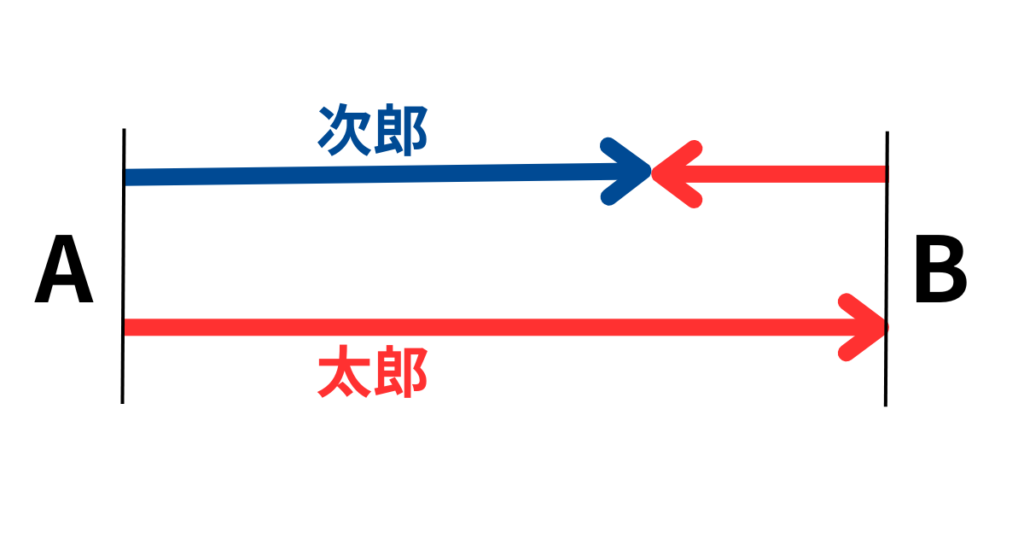
(1)では、A 地点と B 地点を線分の両端として、太郎君と次郎君の進んだ道のりを状況図で表しました。

赤い矢印が太郎君の移動した道のり、青い矢印が次郎君の進んだ道のりです。

まずは、$2$ 人が出会ったのは $x$ 分後として、それぞれの進んだ道のりを矢印の長さで表します。

「道のり＝速さ×時間」なので、赤い矢印の長さは $80\times x$、青い矢印の長さは $60\times x$ です。

次に、$1400$ mを使うために、赤い矢印の長さと青い矢印の長さを足します。$2$ 本の矢印の長さの和が $1400$ mの $2$ 倍になっていることに注意しましょう。

　$80\times x+60\times x=1400\times 2$

分配法則より、

　$(80+60)\times x=2800$

　$x=2800÷(80+60)=20$（分後）

$(80＋60)$ は太郎君と次郎君の速さの和です。したがって、道のりの和を利用する問題では速さの和を使うということがわかります。

旅人算の例題(2)の解説

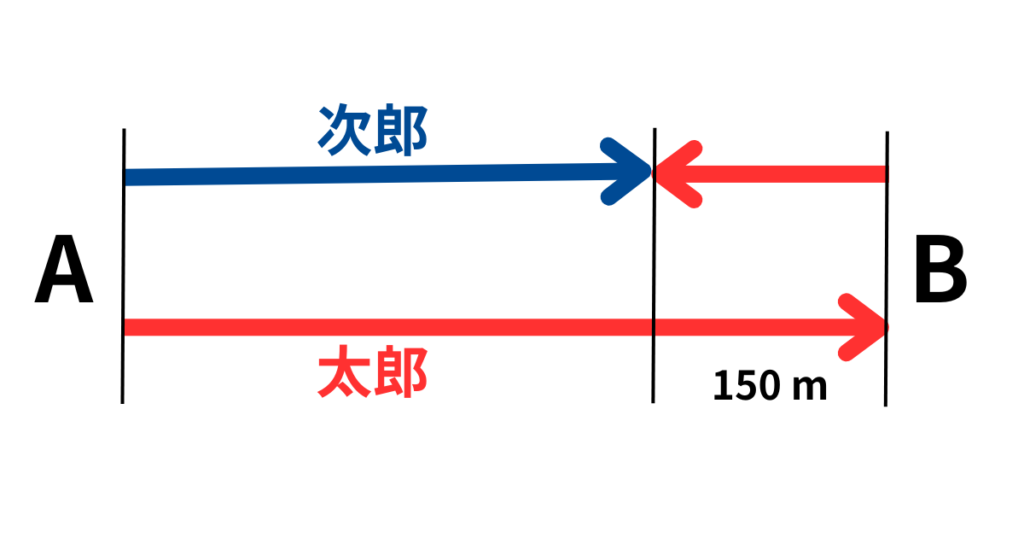
(2)でも、(1)と同じように状況図を描きました。

$2$ 人が出会ったのは $x$ 分後として、赤い矢印の長さは $80\times x$、青い矢印の長さは $60\times x$ です。$150$ mを使うために、赤い矢印の長さから青い矢印の長さを引きます。ここが、(1)とは違うところです。また、$2$ 本の矢印の長さの差が $150$ mの $2$ 倍になっています。

　$80\times x-60\times x=150\times 2$

分配法則より、

　$(80-60)\times x=300$

　$x=300÷(80-60)=15$（分後）

$80-60$ は、太郎君と次郎君の速さの差です。したがって、道のりの差を利用する問題では速さの差を使うということがわかります。

まとめ

旅人算では、道のりの和を考えるときに速さの和を使います。一方、道のりの差を考えるときには速さの差を使います。

「出会い」か「追い越し」かは関係ありません。しかし、多くの算数の問題集や参考書には、

「2人が出会う場合は速さの和を使う出会い算で、1人がもう1人を追い越す場合は速さの差を使う追い越し算です」

としか書かれていません。そのため、受験生は「出会い」「追い越し」という言葉に引きずられてしまいます。

旅人算で「速さの和を使うの？差を使うの？」と悩んでしまう受験生は、「出会い」「追い越し」という言葉を無視するとよいでしょう。そして、状況図を描くなどして、道のりの和と差のどちらを考えればいいのかに注目しましょう。そうすれば、速さの和と差のどちらを使うのかがわかるはずです。