小学5年生で初めて扱うのが円周率です。
小学校の算数では「円周率
しかし、ただ数字を暗記するのではなく、「円周率とは何なのか」といった根本的な部分や円周率の求め方を知っていると算数の勉強がより楽しくなるでしょう。
円周率とは?
円周率は、
「(円周の長さ)
で求められます。
円周率は「円の直径と円周の長さの比」というように定義されます。
円周率が
円周率を求める公式はさまざまな問題で活用できるので、しっかり覚えておきましょう。
円周率の近似値を求めてみよう
円周率は近い値を求めようとすればするほど計算が大変になりますが、今回は正十二角形を用いて近似値を求めてみようと思います。
半径
STEP1 内接する正十二角形の1辺を求める
半径が
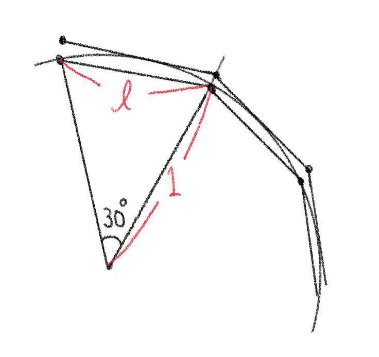
STEP2 中心から外接する正十二角形の頂点までの距離を求める
また、中心から外接する正十二角形の頂点までの距離を
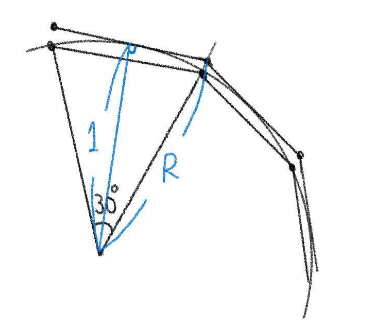
図より、
半角の公式より
よって、
STEP3 外接する正十二角形の1辺を求める
したがって、外接する正十二角形の
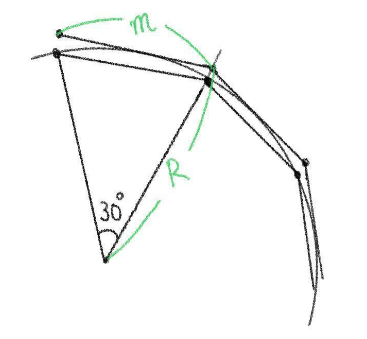
STEP4 円周率の近似値を求める
ここで、
(内接する正十二角形の外周)
よって、
であることがわかります。今回使用した正十二角形の角数を増やせばより円周率に近い値を取ることができます。
おわりに
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。


