【因数分解】交代式、対称式の因数分解

対称式と交代式

今回は因数分解の中でも、どうやって解けばいいか思いつきにくい「交代式」と「対称式」に関する問題を扱います。

一般的にまず対称式とは、 $a$ 、 $b$ 、 $\cdots$ という文字が使われた多項式において、$a$ 、 $b$ 、 $\cdots$ のどの $2$ つを入れ替えても元の式と同一になる式のことを指します。
例えば $a+b$ や $ab$ などですね。これらの式は $a$ と $b$ を入れ替えても式が変わりませんね。

※ちなみに $a+b$ と $ab$ は、 $a$ と $b$ に関する「基本対称式」と言います。
例えば、 $a$ と $b$ と $c$ に関する「基本対称式」であれば、 $a+b+c$ と $ab+bc+ca$ と $abc$ といった具合です。

他にも、 $a^2-ab+b^2$ のように $2$ 乗が含まれていても、もちろん $3$ 乗が含まれていても、対称式を作ることができます。

次に交代式とは、$a$ 、 $b$ 、 $\cdots$ のどの $2$ つを入れ替えても符号だけが変わる式のことを指します。対称式と似ているようで少しだけ違いがありますね。

文面だけでは想像しにくいと思うので、具体的な問題で実際に見ていき、解き方とともに一緒に学んでいきましょう。

対称式と交代式（問題）

次の式を因数分解しなさい。

（$1$）$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$

（$2$）$a^2(b+c)+b^2(c+a)+c^2(a+b)+3abc$

対称式と交代式（答案の例）

（$1$）　$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$

　$=(-b+c)a^2+(b^2-c^2)a+bc(c-b)$

　$=-(b-c)a^2+(b-c)(b+c)a-bc(b-c)$

　$=-(b-c)\{a^2-(b+c)a+bc\}$

　$=-(b-c)(a-b)(a-c)$

　$=(a-b)(b-c)(c-a)$

（$2$）　$a^2(b+c)+b^2(c+a)+c^2(a+b)+3abc$

　$=(b+c)a^2+(b^2+c^2+3bc)a+bc(b+c)$

　$=\{a+(b+c)\}\{(b+c)a+bc\}$

　$=(a+b+c)(ab+bc+ca)$

対称式と交代式（解説）

（$1$）

複数の文字が含まれた式を因数分解する際、注意すべき点は他の記事でも紹介していますが、大切なことなので再度掲示しておきますね。

複数の文字が入った因数分解は、

①　ある文字について、降べきの順に並べる
②　定数項に当たる部分を因数分解してみる
③　その後、式全体を見て、再び因数分解できるかを考える

というステップで考えていく！

今回の問題でもこの順序に従って因数分解を考えていきます。
もちろん、すべての問題についてこのやり方が当てはまるわけではありませんが、問題を解くための手段の一つとしては非常に優秀なものなので、ぜひ試してみてください。

一度すべて展開してから、 $a$ について降べきの順に並べると、

$$(-b+c)a^2+(b^2-c^2)a+b{c}^2-b^{2}c)$$

のようになりますね。

次に定数項を因数分解すると、 $bc(c-b)$ となるため、

$$(-b+c)a^2+(b^2-c^2)a+bc(c-b)$$

となり、式全体を見て見ると、 $b-c$ 、$c-b$ などが共通因数としてくくれそうなことがわかります。
※ $a$ の係数が $(b+c)(b-c)$ のように因数分解できるため

共通因数がわかりやすいように式変形すると、

$$-(b-c)a^2+(b+c)(b-c)a-bc(b-c)$$

のようになりますね。（$b-c)$をすべての項に作りました。）

よって、

　$-(b-c)a^2+(b+c)(b-c)a-bc(b-c)$

　$=(b-c)\{-a^2+(b+c)a-bc\}$

　$=-(b-c)\{a^2-(b+c)a+bc\}$

という式変形までくるはずです。（最後は $-1$ でくくりました。）

あとは、中かっこの中を因数分解します。積が $bc$ 、和が $-(b+c)$ つまり $-b-c$ になる組み合わせは、単純に $-b$ と $-c$ なので、

　$=-(b-c)(a-b)(a-c)$

あとは、先頭にマイナスが付くことがあまりきれいではないことや並び順をもっとスマートにできるという理由から、マイナスを $a-c$ にかけ、因数の順番を入れ替えて、

　$=(a-b)(b-c)(c-a)$

（$2$）

$1$ 同様、ひとまず降べきの順に並べ、定数項を因数分解するところまで行うと、

$$(b+c)a^2+(b^2+c^2+3bc)a+bc(b+c)$$

のように式変形できるはずです。

あとは全体を見て因数分解できないかを考えますが、今回の因数分解は思いつくのが難しいかもしれません。（下の図を参照）

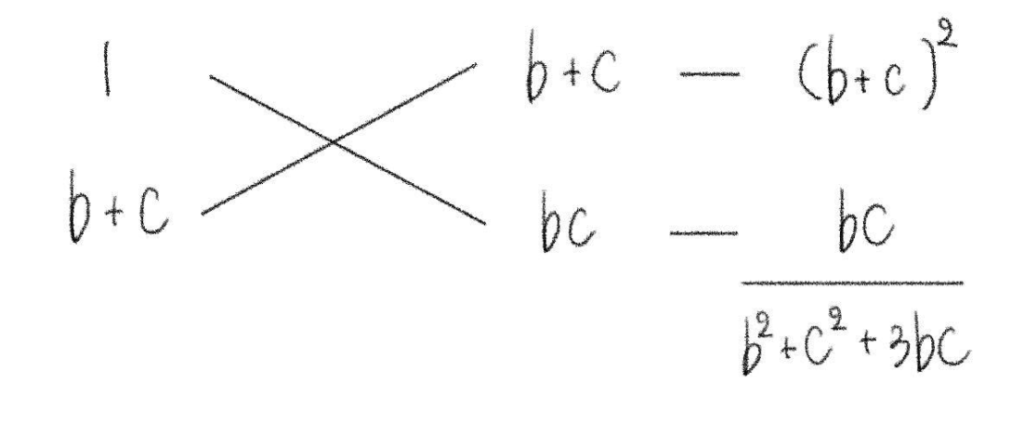
これにより、

$$=\{a+(b+c)\}\{(b+c)a+bc\}$$

となるので、かっこを付けずに表現できるところがあるのでもう少し式変形し、

$$=(a+b+c)(ab+bc+ca)$$

となります。

対称式、交代式に関わらず、基本的には因数分解のステップは変わらないわけですね。
いろいろな因数分解の問題がありますが、ぜひ柔軟に対応していってほしいと思います。

おわりに