3つの集合の共通部分、和集合
\(3\) つの集合の共通部分や和集合を求める際の一般的な考え方について説明します。
集合の演算には、交差(共通部分)、和集合、補集合などがあります。ここでは、特に \(3\) つの集合に関して、これらの演算をどう扱うかを具体的に見ていきます。
- 交差(共通部分)の求め方
\(3\) つの集合 \(A\)、\(B\)、\(C\) の共通部分 \(A \cap B \cap C\) を求めるには、それぞれの集合の要素がすべて共通している部分を見つけます。
例)
集合 \(A = \{1, 2, 3, 4\}\)、集合 \(B = \{2, 3, 5, 7\}\)、集合 \(C = \{3, 4, 5, 6\}\) があるとします。この場合の共通部分を求めてみます。
・\(A\) と \(B\) の共通部分 \(A \cap B = \{2, 3\}\)
・\(A\) と \(C\) の共通部分 \(A \cap C = \{3, 4\}\)
・\(B\) と \(C\) の共通部分 \(B \cap C = \{3, 5\}\)
\(3\) つすべての集合に共通する要素は \(3\) だけです。したがって、
$$A \cap B \cap C = \{3\}$$
です。
- 和集合の求め方
\(3\) つの集合 \(A\)、\(B\)、\(C\) の和集合 \(A \cup B \cup C\) を求めるには、それぞれの集合の要素をすべて含む集合を作ります。重複する要素は \(1\) 度だけ含みます。
例)
同じく集合 \(A = \{1, 2, 3, 4\}\)、集合 \(B = \{2, 3, 5, 7\}\)、集合 \(C = \{3, 4, 5, 6\}\) について考えます。
・すべての要素をリストアップすると:\(\{1, 2, 3, 4, 5, 6, 7\}\)
したがって、和集合
$$A \cup B \cup C = \{1, 2, 3, 4, 5, 6, 7\}$$
です。
3つの集合の共通部分、和集合(問題)
\(A=\{n|n\) は \(16\) の正の約数 \(\}\),
\(B=\{n|n\) は \(20\) の正の約数 \(\}\),
\(C=\{n|n\) は \(8\) 以下の正の偶数 \(\}\) とする。このとき、次に集合を求めよ。
(1) \(A\cap B\cap C\)
(2) \(A\cup B\cup C\)
(3) \((A\cap B)\cup C\)
(4) \((A\cap C)\cup (B\cap C)\)
>>詳細はこちらから
解説
\(A=\{1, 2, 4, 8, 16\}\)
\(B=\{1, 2, 4, 5, 10, 20\}\)
\(C=\{2, 4, 6, 8\}\)
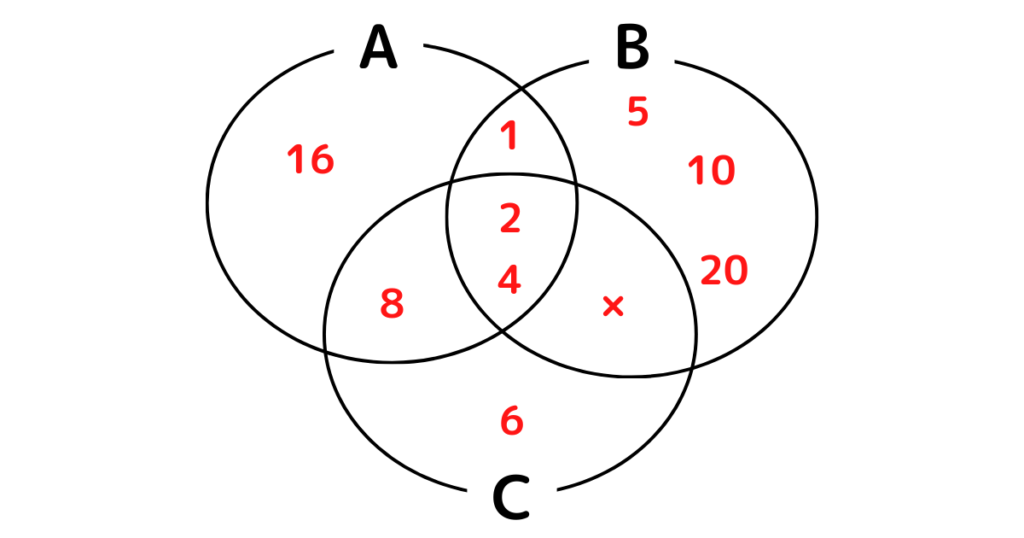
(1) \(A\cap B\cap C\)
\(A\cap B\cap C=\{2, 4\}\)
(2) \(A\cup B\cup C\)
\(A\cup B\cup C=\{1, 2, 4, 5, 6, 8, 10, 16, 20\}\)
(3) \((A\cap B)\cup C\)
\(A\cap B=\{1, 2, 4\}\)
\(C=\{2, 4, 6, 8\}\)
よって、
\((A\cap B)\cup C=\{1, 2, 4, 6, 8\}\)
(4) \((A\cap C)\cup (B\cap C)\)
\(A\cap C=\{2, 4, 8\}\)
\(B\cap C=\{2, 4\}\)
よって、
\((A\cap C)\cup (B\cap C)=\{2, 4, 8\}\)
おわりに
さいごまで読んでいただきありがとうございました!
【最新】こちらの記事がおすすめ!





