関数
真 微分可能
偽 連続

関数
微分可能性と関数の連続性
今回は微分可能性と関数の連続性について解説していきます。
それらについて、微分分野の「微分係数」と「導関数」を解説しながら触れていきます!
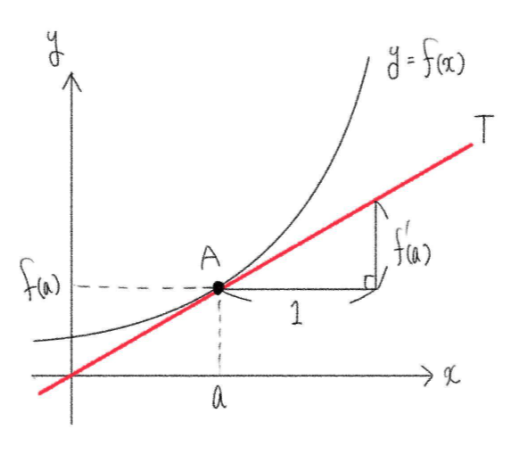
微分係数
① 定義 関数
② 微分可能と連続 関数
解説
① の定義は数学Ⅱで学んだこととまったく同じである。
なお、関数
関数

「② 関数
最終的に、
よって、
ゆえに、
なお、関数
導関数
定義 関数
解説
関数
関数
この新しい関数をもとの関数
記号
などで表す。関数
また、
微分可能性(問題)
次の関数は、[ ] で示された点において連続であるか、微分可能であるかを調べよ。
(1)
(2)
>>詳細はこちらから
微分可能性(解説)
(1)
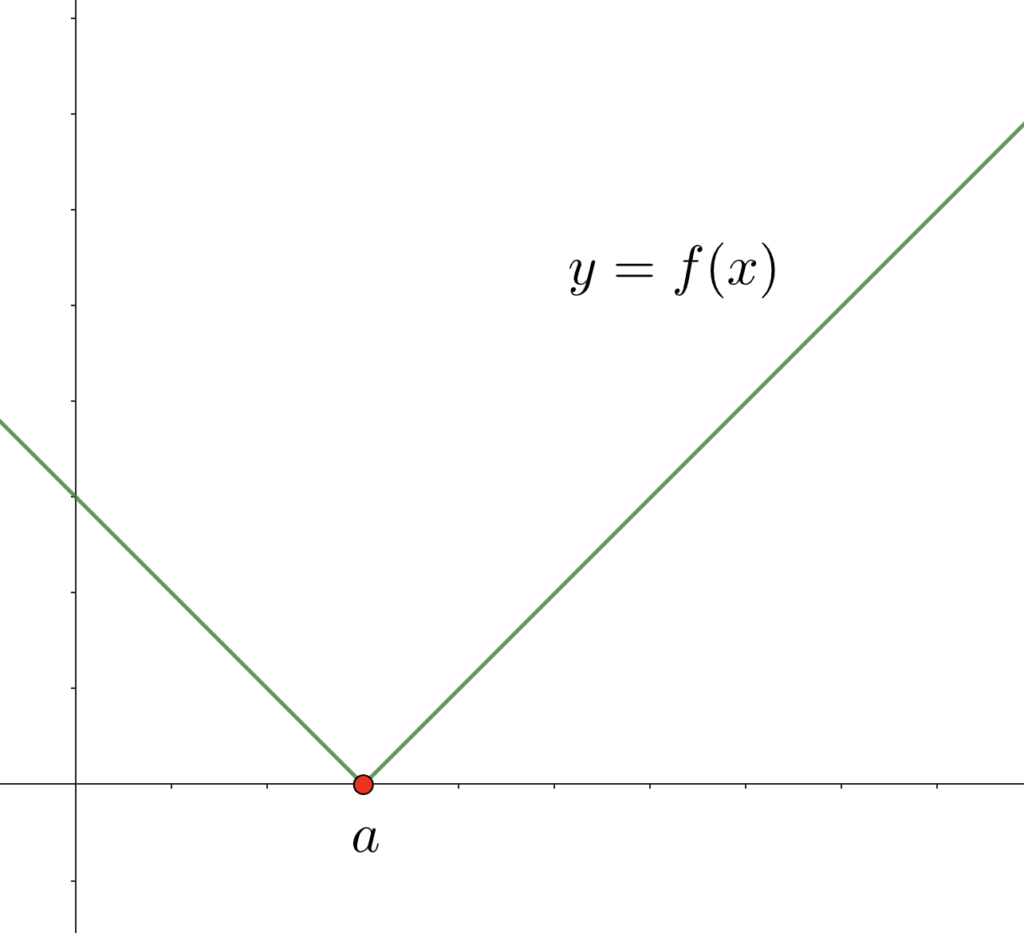

ゆえに、
また、
よって、
次に、
すなわち、
(2)
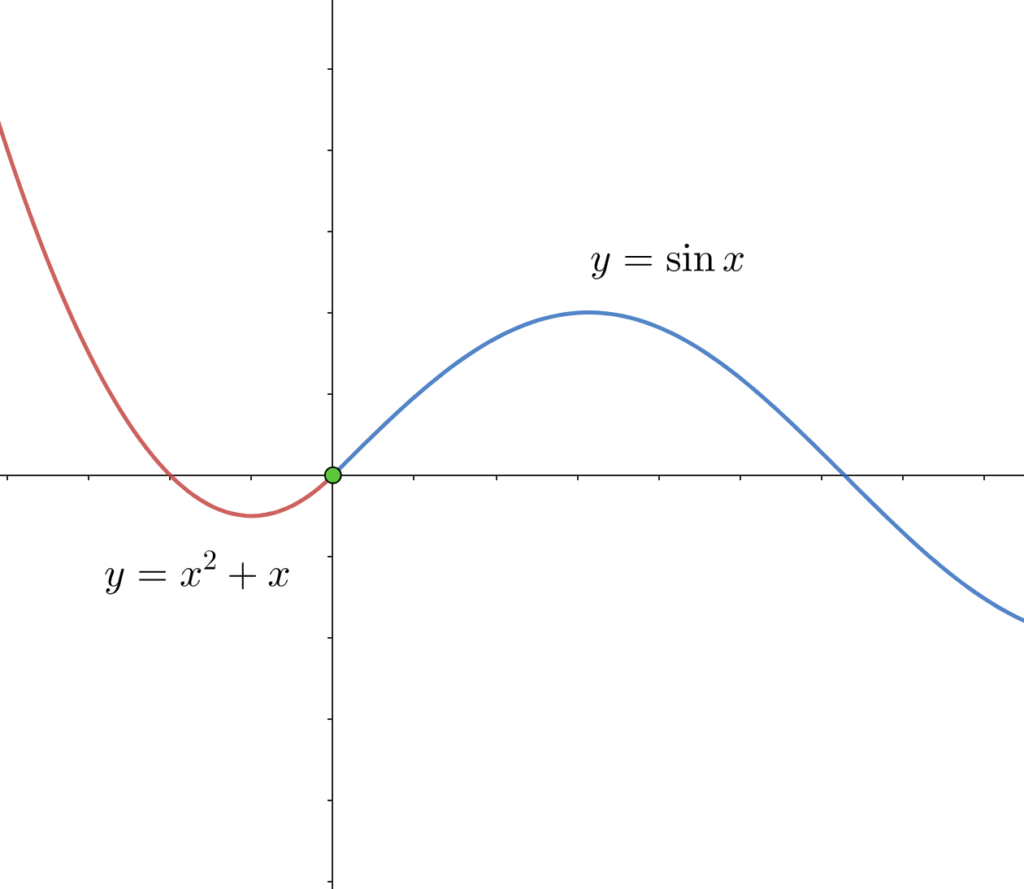

したがって、
おわりに
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。



