【数学】『数学ができない理由とは？』数学が苦手な人の特徴５選

数学を苦手とする人は多くいます。

「数学が得意だから理系に行きます」という人がいる一方で「数学が苦手だから文系に行きます」という人も多くいます。しかし、文系に行ったからといって必ずしも数学とおさらばできるわけではありません。国公立大学に進学するなら共通テストで数学を解く必要がありますし、私立大学でも試験科目で数学を選択できたり、数学の配点が高かったりとなかなか度外視できない科目です。

今回は、数学が苦手な高校生に向けて、数学が苦手な人の特徴とその解決策をまとめてみました。ぜひ、自分と照らし合わせながら読んでみてください！

数学が苦手な人の特徴

一般化できない

「一般化」＝「公式化」

と捉えてもいいかもしれません。

例）\(3x+3=9\)
　　\(3x=9-3\)
　　\(3x=6\)
　　\(x=2\)

この方程式を満たす \(x\) を求めたいので、\(x\) を左辺に残してそれ以外の数字を右辺に移項させます。加減乗除を用いて「\(x=\)」に出来たら完了

この考え方は、数字が変わってももちろんのこと \(x\) 以外の文字であっても同様の方法で解くことができます。

どんな数字であってもどんな文字であっても同じ方法で解く。これが、一般化するということです。

どんな問題にも、規則性や公式、定理などが存在します。それらに則って解く必要があります。

数学が苦手な人は、一般化ができずに数字が変わったり文字が変わったりすると解けなくなってしまいます。つまり、\(3x+3=9\) や \(3a+3=9\)、\(-3x-3=-9\) は全て同じ解法であるにも関わらず、別の問題に見えてしまい、解けなくなってしまいます。

図やグラフを丁寧に描かない

三角比やベクトルなどでは、問題文の内容を図で表す場面が多くあります。また、言うまでもなく関数問題ではグラフを丁寧に描く必要があります。

”丁寧に描く”というのはどういうことでしょう？下の二つの図を見てください。

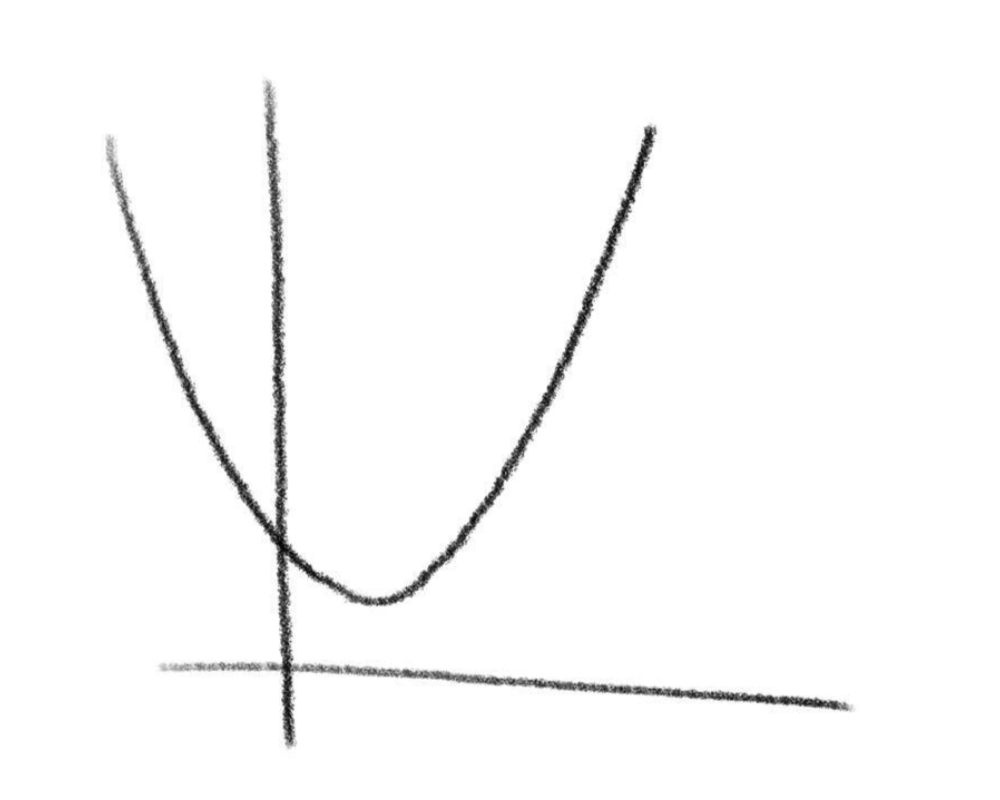
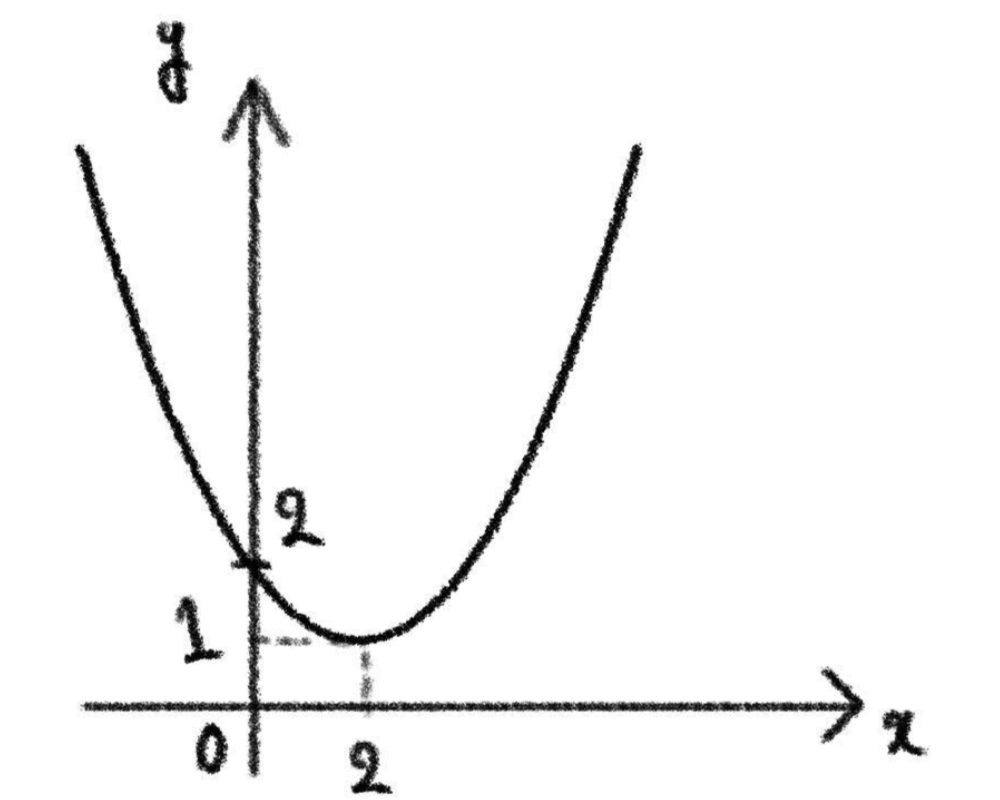
軸の名前や原点などを描かずに減点されたことがある方は多いと思います。左図のように描いても解答に関係ないように思うかもしれませんがそれは大間違いです。その瞬間は必要ないように思ってももう少し先の内容や応用問題になると、軸の名前が変わったり補助線により原点の場所がわかりづらくなったりします。それがミスにつながることもあります。右図のように、しっかりと丁寧に描きましょう。

途中式を丁寧に書かない

図やグラフと同様に、途中式を丁寧に描くこともとても大切です。

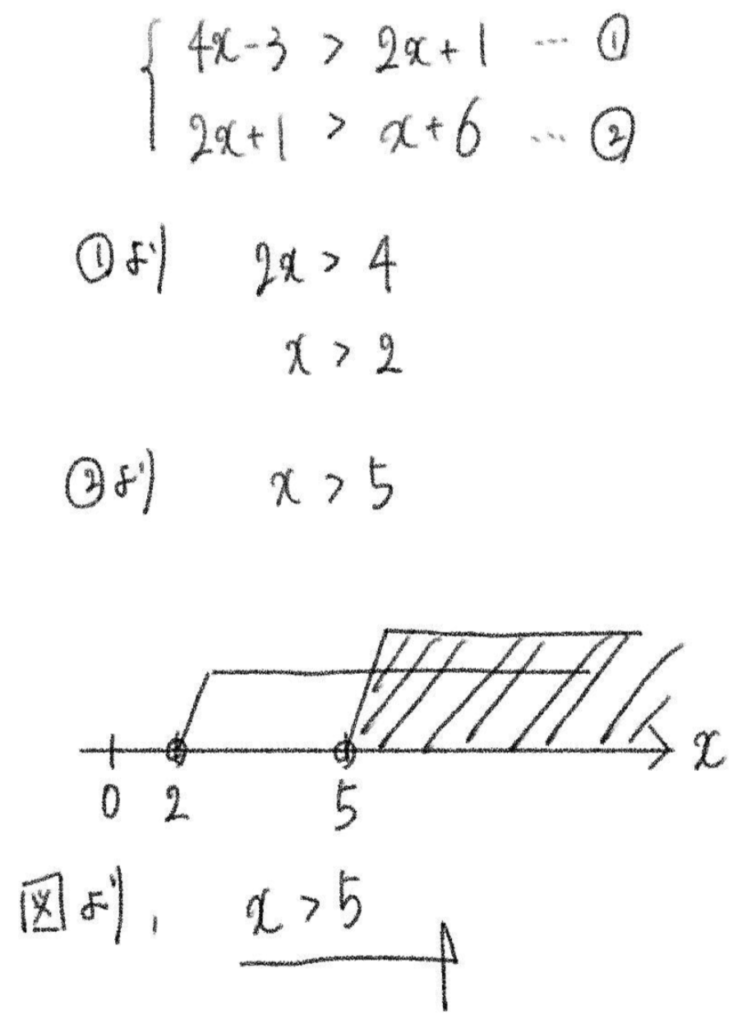
上記の図はどちらも答えは同じですが、右図の方がより丁寧に描かれているのがわかります。答えが同じであれば左図の方が短くて良い気がしますが、途中式を描くことを疎かにしていると、難しい問題になったときに太刀打ちできなくなります。

難しい問題にも対応できるようにするには、簡単な問題であってもしっかりと途中式を描いて解法を理解する必要があります。簡単な問題は、難しい問題に対応するための練習ということですね。

同じ問題を繰り返し行わない

「問題を見て、実際に解いてみて、解答を見て足りなかった部分を補ったり修正する。」これが数学の一般的な勉強方法です。どのステップも非常に大切なもので、飛ばしてはいけません。しかし、テスト直前だと問題と解答を開いて、ざっくりとした解き方を確認していくなんて勉強を採用してしまいます。

それだと、テスト本番で数字や文字を変えられてしまうと途端に出来なくなってしまいます。

時間をかけてでも、しっかりと頭を使って解きながら進めましょう。

解けた問題の理解度やわからなかった問題にはチェックを付けながら進めましょう！

問題の細部まで読まない

これは数学だけに限った話ではありません。

問題文にはたくさんの情報が隠されています。「問い」だけでなく、その問いを紐解くための条件や設定なども含まれています。

しっかりと読まないと、条件が足りなくて立式できなかったり、値が \(2\) つ以上出てきた時に違う答えを採用してしまったりします。

一語一句抜け漏れなく読みましょう！

数字や、重要な条件には下線や丸などを付けると良いです！

数学苦手を克服するための解決策

上記の \(5\) つを意識すれば克服できる可能性はぐっと上がるはずです。

しかし、「意識すること」と「実行すること」は全く違います。実行に移るまではたくさんの時間を要します。また、実行できたとしても点数に反映されるのもまた時間を要します。

根気強くがんばりましょう！

おわりに