今回は
まずは、「
急に難しい説明をされても挫折してしまいそうなので、
我々の世界で一般的に使われている
※あくまでも私なりの解釈である点ご了承ください。
突然ですがみなさん、かくれんぼで鬼になった時にこう言われた時はありませんか?

じゃあ鬼は10秒数えたら開始にしましょう!



わかりました!10, 9, 8…
これ以外にも、子供の時に「お風呂に10秒浸かりな!」などと言われたことがあるのではないでしょうか?このように、何かと「10」というくくりで数字を扱う場面が多いですよね。それは、我々の世界が基本的には10進数だからだと考えられます!
また、10 というくくりで数えるのは、
「両手の指が合わせて10本だから」
という説もあります。(本当のところは分かりません…)
我々の世界は10進数ですが、他にも時計は
例えば、
※
すべての数は
と表すことができます。特に、
n進数の四則演算
例)
例)
<参考①>
[
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 10 |
| × | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
例)
<参考②>
[
| + | 1 | 2 | 3 | 4 |
| 1 | 2 | 3 | 4 | 10 |
| 2 | 3 | 4 | 10 | 11 |
| 3 | 4 | 10 | 11 | 12 |
| 4 | 10 | 11 | 12 | 13 |
| × | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 4 | 11 | 13 |
| 3 | 3 | 11 | 14 | 22 |
| 4 | 4 | 13 | 22 | 31 |
例)
例題 ① 他の記数法で表す
>>詳細はこちらから
(解説)
(解法1)
※
よって、
(解法2)
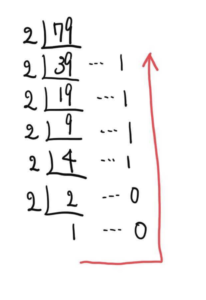

図のように、筆算の割り算を縦にしていく。そして、下から矢印の方向に数字を並べていくと答えになる。
よって、
(解法1)
※
よって、
(解法2)
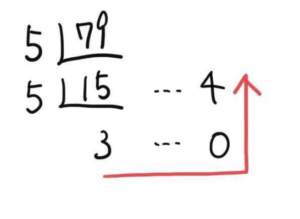
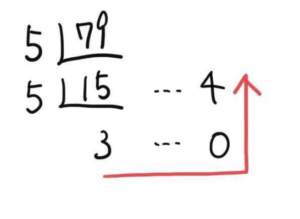
図のように、筆算の割り算を縦にしていく。そして、下から矢印の方向に数字を並べていくと答えになる。
よって、
例題 ② n進数の四則演算
次の計算の結果を、[ ]内の記数法で表せ。
(1)
(2)
(3)
(解説)
(1)
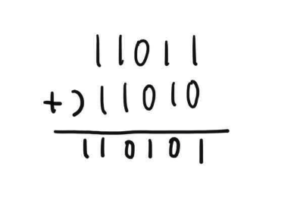
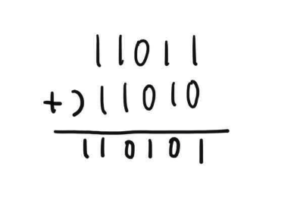
(2)
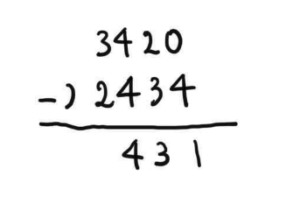
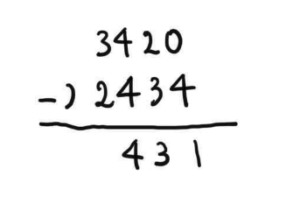
下の数字の方が大きい場合は、1つ大きい位から繰り下げます。そして、繰り下げたら
(3)
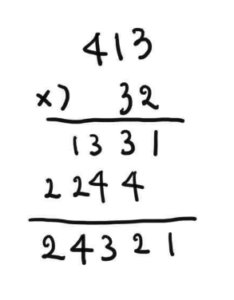
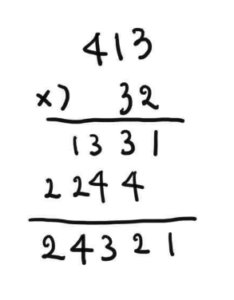
例)
おわりに
今回は、
・一般的に、
と表すことができる。特に、
・
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。



