【統計学の基礎】幾何分布

少し数字に強い理系大学卒から駆け出しデータアナリストになるまでに、実際に読んだ50冊以上の本から厳選して、基本的な理論から実践的スキルまでを身につけられるようにデータ分析初学者向けにまとめました。＞＞記事を読む

幾何分布とは

幾何分布は、試行が成功するまでにかかる回数を表す離散分布です。

ここでの「成功」とは、特定の条件を満たす事象のことを指し、各試行は成功確率が一定で独立していると仮定します。

例えば、サイコロを振って「$1$」が出るまでの回数をモデル化する際に、幾何分布が用いられます。

幾何分布の特徴は、失敗が連続した後に、特定の試行で初めて成功するまでの回数に関する確率を表現できる点です。この分布は、試行回数 $X$ がある正の整数であり、$1$ 回の試行で成功する確率が一定の $p$ であると仮定した場合に適用されます。

$$P(X = k) = (1 – p)^{k-1} \cdot p$$

この式の意味を簡単に説明すると、最初の $k-1$ 回は失敗する確率 $1 – p$ が連続し、最後の $k$ 回目に成功する確率 $p$ を掛け合わせたものです。

さいころを投げて初めて $1$ が出るまでの回数 $X$ の確率 $P(X)$ を表にまとめました。

スクロールできます

$X$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$
$P(X)$	$0.167$	$0.139$	$0.116$	$0.096$	$0.080$	$0.067$	$0.056$	$0.047$	$0.039$	$0.032$

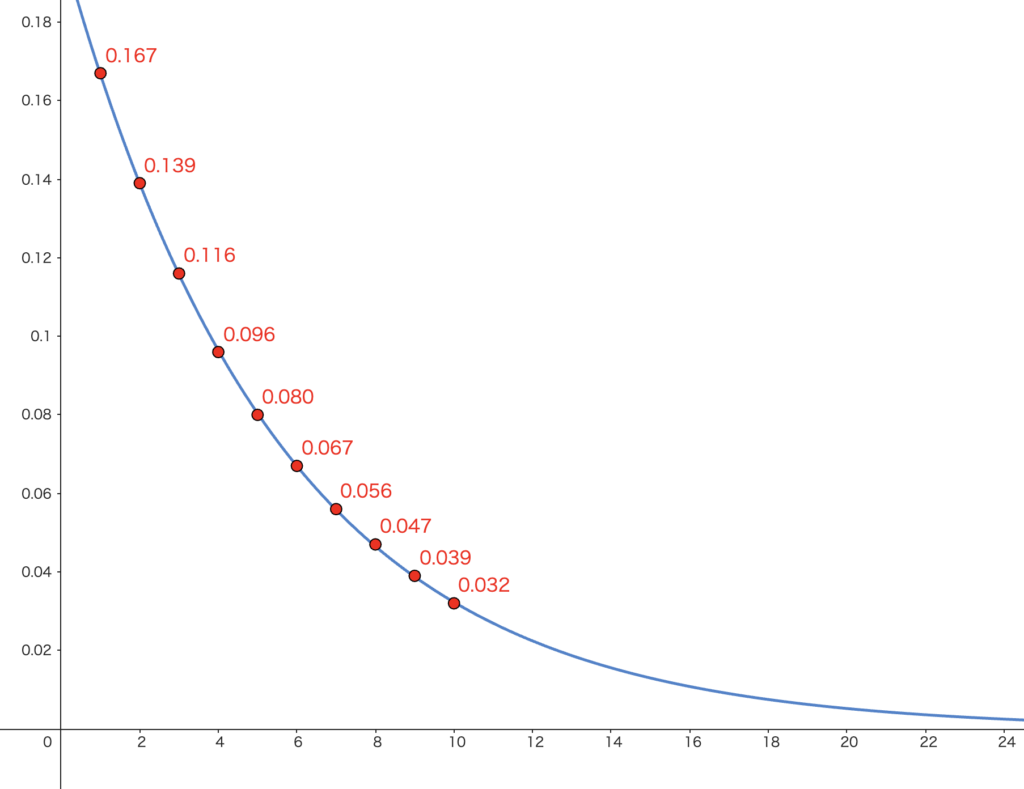
分布より、$1$ が現れる確率は初回が一番高くて、回数を重ねるほどに低くなっていくことがわかりますね。

▽期待値の導出

幾何分布の期待値 $E(X)$ は、成功までの試行回数の平均を表します。この期待値は次の式で計算されます。

$$E(X) = \frac{1}{p}$$

期待値は、すべての試行回数における期待される成功までの回数の平均値をとり、次のように計算されます。

$E(X) = \sum_{k=1}^{\infty} k \cdot P(X = k)$

　$= \sum_{k=1}^{\infty} k \cdot (1 – p)^{k-1} \cdot p$

この計算を進めると、最終的に期待値 $E(X) = 1 / p$ が得られます。期待値の導出には無限等比数列の和などが使われ、幾何分布の特性を活かした計算が必要です。

▽分散の導出

幾何分布の分散 $V(X)$ は次の式で表されます。

$$V(X) = \frac{1 – p}{p^2}$$

幾何分布の分散は、次のように期待値を用いて計算されます。

$$V(X) = E(X^2) – [E(X)]^2$$

ここで $E(X^2)$ は、二乗した試行回数の期待値であり、計算には幾何級数が用いられます。結果として、幾何分布の分散が $V(X) = \frac{1 – p}{p^2}$ という式に導かれます。

幾何分布は、以下のような実生活やビジネスでのさまざまな場面で活用されています。

(1) 品質管理

製造業では、製品の品質を管理するために不良品が出るまでの回数をモニタリングする際に幾何分布を使います。特に、製造ラインで製品を1つずつ検査していき、不良品が発生するまでの試行回数がどのような分布になるかを分析することで、製品の品質や検査方法の改善につなげることができます。

(2) ベイズ推定における事前分布

幾何分布は、ベイズ推定においても利用されます。特に、成功・失敗を繰り返す実験において、成功までの試行回数を考慮した信念を表現する際に用いられ、結果の確率を推定するための基礎分布として重要な役割を果たします。

(3) 顧客行動分析

幾何分布はマーケティング分野においても活用され、例えば「顧客が初めて商品を購入するまでの訪問回数」などの分析に使われます。特定の商品を顧客が初めて購入するまでの回数に注目することで、購買行動の傾向を分析し、マーケティング施策の最適化に役立てます。

(4) コンピュータサイエンスやアルゴリズムの性能評価

幾何分布は、ランダムに行う試行における「成功」までの回数を考えるため、アルゴリズムの性能評価にも利用されます。特に、ランダムなイベントを伴うアルゴリズムの成功率を評価する場合、試行回数が幾何分布に従うケースが多く、パフォーマンスを予測するために使われます。

幾何分布は、試行が成功するまでの回数をモデル化する離散分布で、確率関数や期待値、分散が計算されることでその特性が明らかになります。

試行回数が増えるほど成功確率が下がるため、様々な場面での分析や品質管理、マーケティングなどの分野で役立っています。幾何分布の知識を深め、活用することで、試行回数やリスク管理に関する判断がしやすくなるでしょう。

さいごまで読んでいただきありがとうございました！

このブログは統計学を学びたい学生/社会人向けに記事を書いています。

【最新】こちらの記事がおすすめ！

\(X\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
\(P(X)\)	\(0.167\)	\(0.139\)	\(0.116\)	\(0.096\)	\(0.080\)	\(0.067\)	\(0.056\)	\(0.047\)	\(0.039\)	\(0.032\)