ロジスティック回帰分析の基礎と応用
ロジスティック回帰分析は、統計学や機械学習の分野で広く用いられる手法の一つです。
特に二値分類問題に適しており、データに基づいて結果を予測するのに役立ちます。本記事では、ロジスティック回帰の基本概念、計算式、そして実際の応用例について説明します。
ロジスティック回帰とは?
ロジスティック回帰は、目的変数が二値(
ロジスティック回帰では、シグモイド関数を用いて確率をモデル化します。
シグモイド関数は、次のように定義されます。
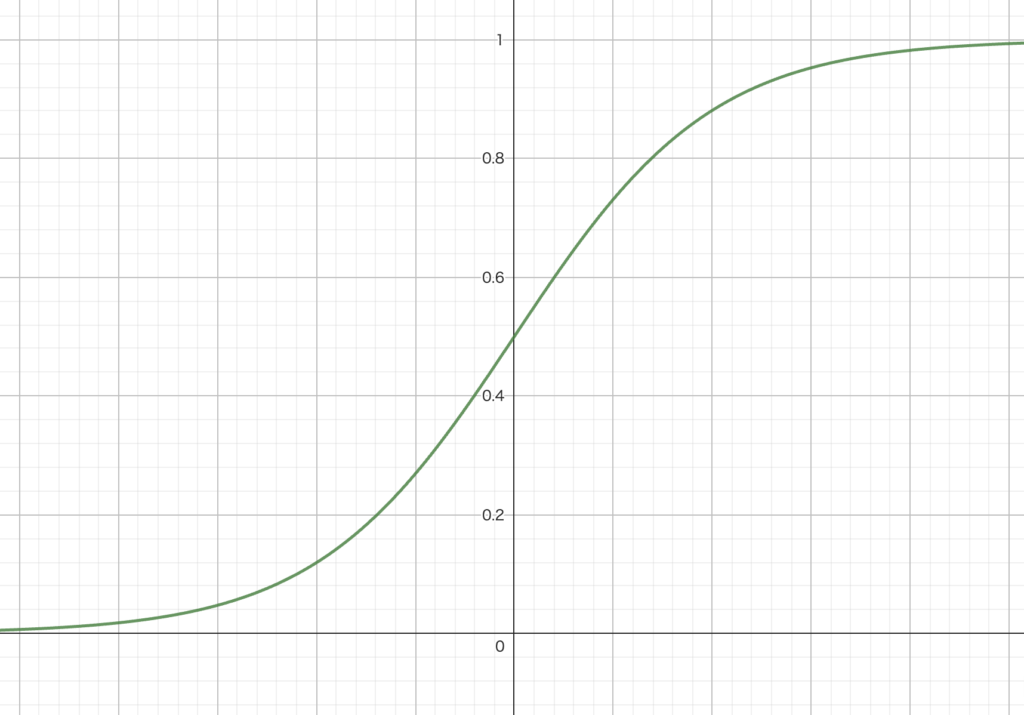
ここで、
ロジスティック回帰の計算式
ロジスティック回帰モデルの目的は、入力変数 (
この確率は以下のように表されます。
これを簡単にすると、
このモデルを最適化するために、対数尤度関数を最大化します。
対数尤度関数は以下の通りです。
ロジスティック回帰の応用例
応用例1: スパムメールの分類
スパムメールの分類は、ロジスティック回帰の典型的な応用例です。ここでは、メールの特徴(例:特定の単語の出現頻度、送信者アドレスのドメインなど)を入力変数として、メールがスパムか否かを予測します。
<div class="hcb_wrap"><pre class="prism line-numbers lang-python" data-lang="Python"><code># Pythonでの簡単な例
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# データの読み込み
data = pd.read_csv('spam_data.csv') # CSVファイルからデータを読み込む
X = data[['feature1', 'feature2', 'feature3']] # 特徴量として使用する列を指定
y = data['is_spam'] # 目的変数(スパムかどうか)を指定
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# データを訓練データとテストデータに分割。全データの20%をテストデータとして使用
# モデルの訓練
model = LogisticRegression() # ロジスティック回帰モデルを作成
model.fit(X_train, y_train) # 訓練データを用いてモデルを訓練
# 予測と評価
y_pred = model.predict(X_test) # テストデータを用いて予測を実行
print("Accuracy:", accuracy_score(y_test, y_pred)) # 予測結果の精度を表示</code></pre></div>1. データの読み込み: pd.read_csv関数を使ってデータを読み込みます。
2. 特徴量とラベルの設定: 分類に使用する特徴量(列)と、目的変数(スパムかどうか)を設定します。
3. データの分割: train_test_split関数を使って、データを訓練データとテストデータに分割します。テストデータは全体の20%としています。
4. モデルの訓練: LogisticRegressionクラスを使ってロジスティック回帰モデルを作成し、訓練データを用いてモデルを訓練します。
5. 予測と評価: 訓練されたモデルを使ってテストデータを予測し、accuracy_score関数を使って予測の精度を評価します。
応用例2: 医療データの診断
患者のデータ(年齢、性別、検査結果など)を用いて、特定の病気の有無を予測することもロジスティック回帰で可能です。例えば、心臓病のリスクを予測するモデルを構築できます。
# Pythonでの医療データ診断の例
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
# データの読み込み
data = pd.read_csv('medical_data.csv') # CSVファイルからデータを読み込む
# 特徴量とラベルの設定
X = data[['age', 'blood_pressure', 'cholesterol', 'gender']] # 特徴量として使用する列を指定
y = data['has_disease'] # 目的変数(病気の有無)を指定
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# データを訓練データとテストデータに分割。全データの20%をテストデータとして使用
# モデルの訓練
model = LogisticRegression() # ロジスティック回帰モデルを作成
model.fit(X_train, y_train) # 訓練データを用いてモデルを訓練
# 予測
y_pred = model.predict(X_test) # テストデータを用いて予測を実行
# 評価
accuracy = accuracy_score(y_test, y_pred) # 予測結果の精度を計算
conf_matrix = confusion_matrix(y_test, y_pred) # 混同行列を計算
class_report = classification_report(y_test, y_pred) # 分類レポートを生成
print("Accuracy:", accuracy) # 精度を表示
print("Confusion Matrix:\n", conf_matrix) # 混同行列を表示
print("Classification Report:\n", class_report) # 分類レポートを表示1. データの読み込み: pd.read_csv関数を使ってデータを読み込みます。
2. 特徴量とラベルの設定: 分類に使用する特徴量(年齢、血圧、コレステロール値、性別)と、目的変数(病気の有無)を設定します。
3. データの分割: train_test_split関数を使って、データを訓練データとテストデータに分割します。テストデータは全体の20%としています。
4. モデルの訓練: LogisticRegressionクラスを使ってロジスティック回帰モデルを作成し、訓練データを用いてモデルを訓練します。
5. 予測: 訓練されたモデルを使ってテストデータを予測します。
6. 評価: accuracy_score関数を使って予測の精度を評価し、confusion_matrix関数を使って混同行列を計算し、classification_report関数を使って分類レポートを生成します。
まとめ
ロジスティック回帰分析は、二値分類問題において非常に有用な手法です。シグモイド関数を用いた確率のモデル化により、複雑なデータセットに対しても効果的に予測を行う。
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。


