クラスタリングとは
クラスタリングとは、ある集合を非類似度に従って、部分集合（クラスター）に分けることです。
「非類似度」とは、どれくらい似ているか（似ていないか）ということです！
非類似度の定義の仕方は様々です。例えば、以下のような図形の集合があったとしましょう。
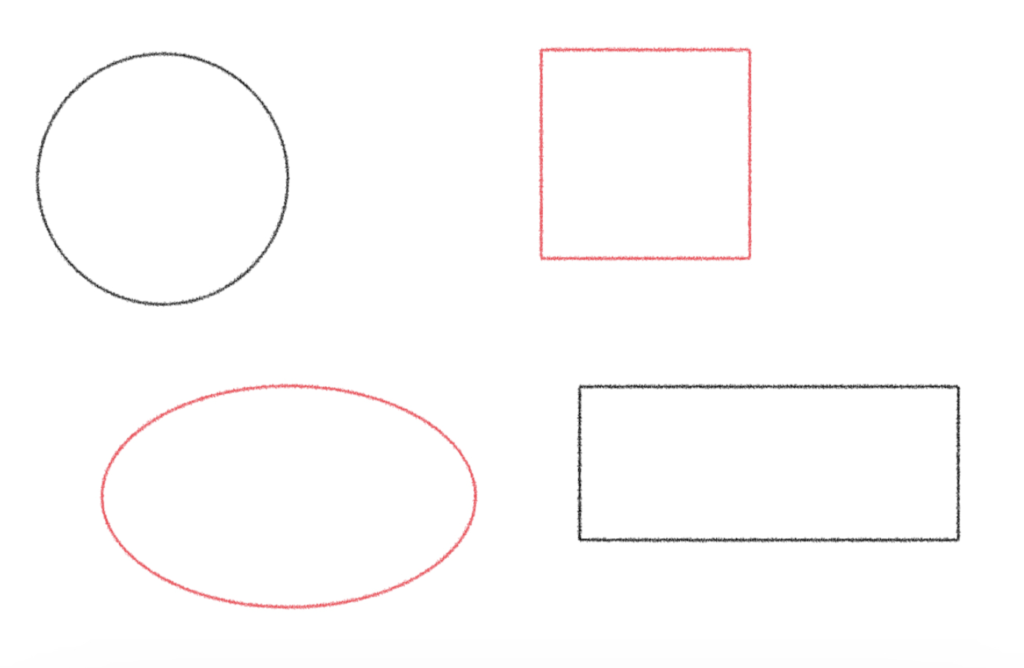
「形」を基準にすると、
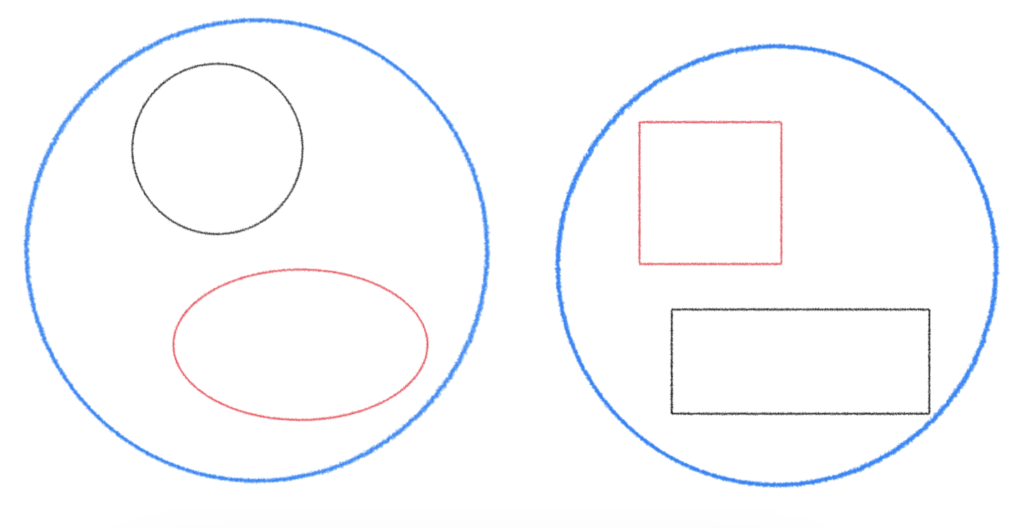
「色」を基準にすると、
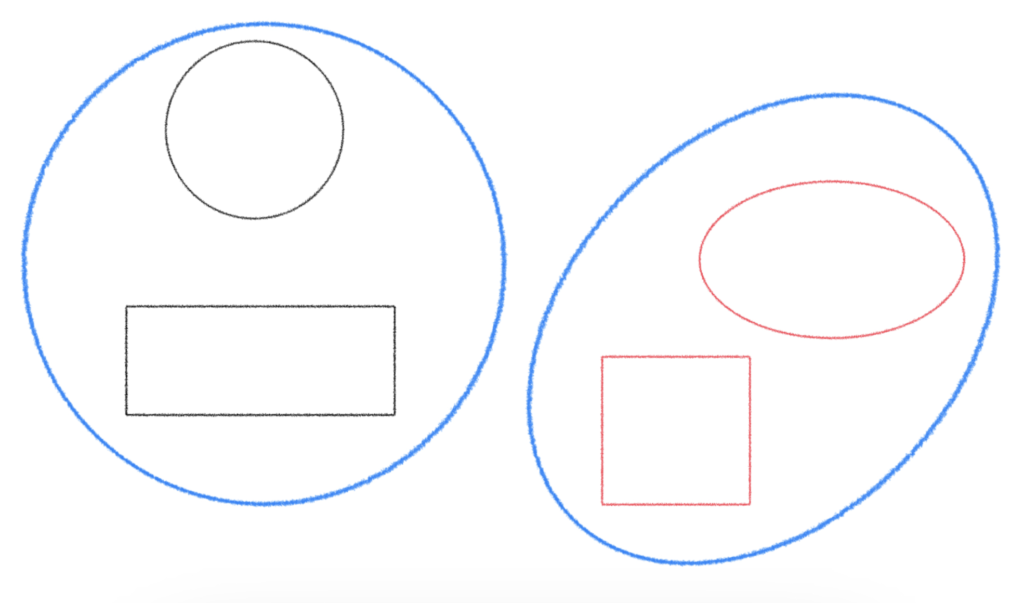
このように、分けるための基準を非類似度、あるいは類似度や単に距離と呼ぶこともあります。
クラスタリングには大きく 2 つに分けられます。
・階層的手法
樹形図によって表現されるような、集団の系統発生的な構造をさぐることによってクラスターを構成しようとするものです。各個体を \(1\) つのクラスターとして、ある基準に従って結合していく凝集型と分類すべき集合を \(1\) つのクラスターとしてある基準に従って分裂していく分裂型の \(2\) つに大別される。
・非階層的手法
クラスターの妥当性の基準として、クラスター内の変動をできるだけ小さくし、クラスター間の変動をできるだけ大きくしようとし、あらかじめクラスター数が決まっているような手法です。
クラスタリングを考える上で重要な \(3\) つの事柄
・個体間の類似度/非類似度
・算法（アルゴリズム）
・評価
個体間の類似度
扱うデータによって、類似度（距離）の定義は様々ですが、一般的には以下の \(3\) つが挙げられます。
ある個体を、\(x=(x_1\), \(x_2)\) と \(y=(y_1\), \(y_2)\) とすると、
\(L_1\) 距離（直角距離）
\(D(x, y)=|x_1-y_1|+|x_2-y_2|\)
\(L_2\) 距離（ユークリッド距離）
\(D(x, y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}\)
\(L_{\infty}\) 距離（チェビシェフ距離）
\(D(x, y)=\max \{|x_1-y_1|\), \(|x_2-y_2|\}\)
\(l_2\) 距離（ユークリッド距離）は中学で学ぶ一番馴染み深い距離かなと思います。
このように、扱うデータによって様々な距離が存在しています！
算法（アルゴリズム）
クラスター分析には、さまざまなアルゴリズムが存在します。ここでは、代表的なアルゴリズムとして、K-means法、階層型クラスタリング、DBSCANなどが挙げられますが、今回は、非階層的手法に絞って紹介していきます。
K-means法は、非階層的クラスタリング手法の中でも最も広く使われる手法で、最小二乗法に基づいてクラスターを構築します。理論的な視点からK-means法の手順を解説し、その応用例も示します。
K-means法の理論的手順
K-meansでは、最初にデータ空間において \(K\) 個のクラスター数を設定します。\(K\) はユーザーが事前に決定するパラメータです）。初期クラスター中心（セントロイド）は、ランダムに \(K\) 個のデータポイントから選ばれます。
次に、各データポイントが最も近いセントロイドに割り当てられます。これを行う際、各データ点 \(x\) がセントロイド\(μ_k\) にどれだけ近いかを、ユークリッド距離や他の距離尺度に基づいて計算します。
$$d(x, \mu_k) = || x – \mu_k ||^2$$
データ点は、この距離が最も小さいセントロイドを持つクラスターに割り当てられます。
クラスターの割り当てが終わった後、それぞれのクラスターの中心（セントロイド）が再計算されます。新しいセントロイドは、そのクラスターに属するデータ点の平均値として計算されます。
$$\mu_k = \frac{1}{|C_k|} \sum_{x_i \in C_k} x_i$$
ここで、\(C_k\) はクラスター \(k\) に属するデータ点の集合です。この再計算されたセントロイドは、次のクラスター割り当てに使用されます。
STEP2とSTEP3を繰り返し、クラスター割り当てやセントロイドの位置が変わらなくなる、つまり、収束条件が満たされるまで処理を続けます。収束条件には以下のようなものがあります。
・クラスターの割り当てが変わらなくなる
・セントロイドの移動距離が小さくなる
K-meansの目標は、全てのデータポイントのセントロイドへの距離の二乗和を最小化することです。
$$J = \sum_{k=1}^{K} \sum_{x_i \in C_k} || x_i – \mu_k ||^2$$
この関数Jを最小にするようにクラスターを構成することが、K-meansの最終目的です。
K-means法の応用例
応用例1: 顧客セグメンテーション
マーケティング分野では、K-means法を用いて顧客を特定の属性に基づいてグループ化し、マーケティング戦略を最適化することが一般的です。たとえば、顧客の購買履歴や年齢、収入などのデータを基に、同じ特性を持つ顧客をクラスターに分けることができます。これにより、各グループに対してターゲットを絞ったキャンペーンやサービスを提供できるようになります。
応用例2: 画像圧縮
K-means法は、画像圧縮にも応用されます。画像をピクセルの集まりとして扱い、ピクセルの色をK個の代表的な色（クラスターのセントロイド）に分類することで、色の数を減らして画像を圧縮します。この手法は、コンピュータビジョンや画像処理の分野でよく使用されます。
応用例3: 異常検知
K-means法は異常検知にも用いられます。例えば、センサーデータや金融取引データなどに対してK-means法を適用し、データをクラスターに分類します。通常のデータはクラスターの中心に近く、異常なデータはクラスターの外れに位置するため、クラスターのセントロイドから遠く離れたデータを異常として検出することができます。
クラスターの評価方法
クラスター分析の結果を評価するための手法について説明します。例えば、シルエット係数やダビッド・バウディン指数など、クラスターの質を測る指標があります。これらの評価方法を使用して、クラスターの分割が適切かどうかを判断するプロセスを解説します。
おわりに
さいごまで読んでいただきありがとうございました！
【最新】こちらの記事がおすすめ！