【確率分布と統計的な推測】母平均の推定をわかりやすく解説

母平均の推定

一般的に、母集団（調査対象の集団）の大きさが大きいときには、それらの分布を調べることは簡単ではありません。そこで、母集団分布の母平均や母比率を効果的に、かつ誤差が少なく推定する方法について考えることが必要になります。

もう少しわかりやすく言うなら、

ということです。

また、抽出した値から全体の平均を幅を持たせて求める際に信頼区間を用います。

例えば、平均は $25$ というように断言するのではなく、$[18$,　$32]$ といった感じです。

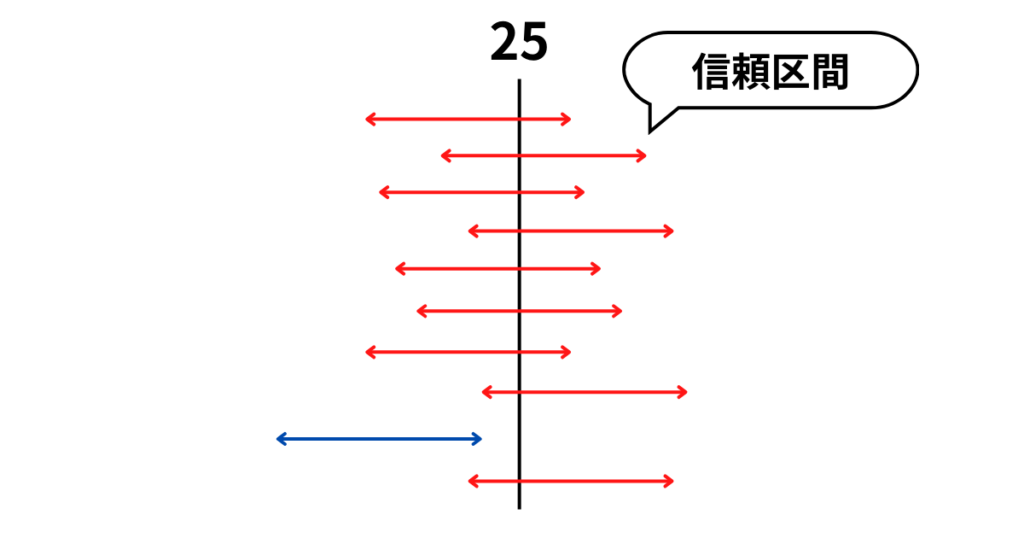
詳細を説明していきます！

信頼区間

標本の大きさ $n$ が大きいとき、母平均 $m$ に対する

　母平均の推定（問題）

ある工場で大量生産されている電球の中から無作為に抽出した $25$ 個について試験したところ、それらの寿命の平均値は $1500$ 時間であった。製品全体の平均寿命を信頼度 $95$ % で推定せよ。ただし、製品の寿命は正規分布に従い、標準偏差は $110$ 時間である。

解説

標本の大きさ：$n=25$
標本平均：$\bar{X}=1500$
母標準偏差は：$\sigma =110$

製品の寿命は正規分布に従うから、標本平均 $\bar{X}$ は正規分布 $N(m$,　${\displaystyle \frac{{\sigma }^2}{n})}$ に従う。

$$Z={\displaystyle \frac{1500-m}{\frac{110}{\sqrt{25}}}=\frac{1500-m}{22}}$$

$$f(|Z|\le c)=2f(Z\le c)=0.95$$

$f(Z\le c)=0.475$ となる $c$ は、正規分布表より $1.96$ となる。

$$\begin{array}{rcl}f(-1.96\le Z\le 1.96)& =& f(-1.96\le {\displaystyle \frac{1500-m}{22}\le 1.96)}\\ & =& f(-1.96\cdot 22\le 1500-m\le 1.96\cdot 22)\\ & =& f(-1.96\cdot 22-1500\le -m\le 1.96\cdot 22-1500)\\ & =& f(1500-1.96\cdot 22\le m\le 1500+1.96\cdot 22)\\ & =& f(1456.88\le m\le 1543.12)\end{array}$$

よって、信頼度 $95$ % の信頼区間は、$[1457$,　$1543]$

おわりに