【能登半島地震M7.6を観測】マグニチュードと震度の違いとマグニチュードの求め方

マグニチュードと震度の違い

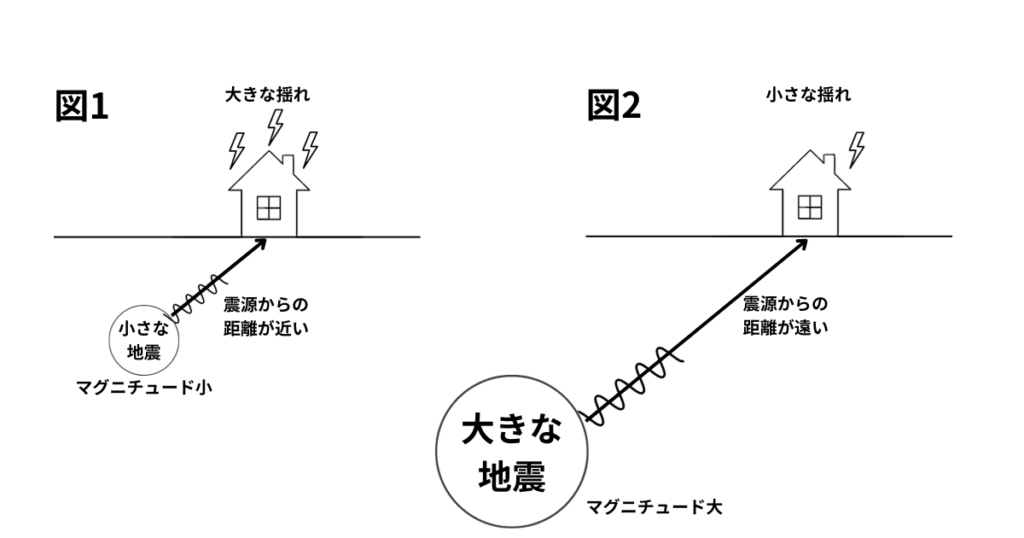
マグニチュードが大きければ震度も大きくなるとは限りません。

マグニチュードが小さい地震でも震源からの距離が近いと地面は大きく揺れて、震度は大きくなります。(図1)

また、マグニチュードが大きい地震でも震源からの距離が遠いと地面はあまり揺れなく、震度は小さくなります。(図2)

マグニチュードと地震エネルギーの関係

〈マグニチュードとエネルギーの関係〉

対数を指数に直すと、$E={10}^{4.8+1.5M}$

マグニチュード $7$ と $8$ を比べてみましょう！

差を求めると、${10}^{16.8}-{10}^{15.3}={10}^{1.5}$

よって、マグニチュードが $1$ 大きくなると、地震のエネルギーは、${10}^{1.5}=31.622\cdots$ (倍)

になることがわかります。

つまり、マグニチュードが $2$ 増えると、地震のエネルギーは $32\times 32=1004$ 倍も大きくなるのです。

マグニチュードが大きければ大きいほど地震のエネルギーも大きくなります。エネルギーと言われてもピンとこない人もいると思うので以下を参考にしてみてください。

マグニチュード	エネルギー	備考
	$4184J$	$1$リットルの水を $1^{\circ }C$ 上げるときのエネルギー
$7.3$	$7.94PJ$ $7940$ 兆ジュール	兵庫県南部地震
$8.2$	$125PJ$ $12$ 京 $2500$ 兆ジュール	関東大震災
$9.0$	$2.00EJ$ $200$ 京ジュール	東日本大震災
$9.2$	$3.98EJ$	$2019$ 年日本国内 年間発電量($3.68EJ$)

東日本大震災で発生したエネルギーは、日本国内の年間発電量の約半分です。これを見ても東日本大震災がどれほどの地震だったのかがわかりますね。

マグニチュードについて

モーメントマグニチュード

断層面の剛性率：$\mu$ ($Pa$)
断層面積の合計：$A$（$m^2$）
変異量の平均：$\bar{D}$（$m$）

地震モーメントを $M_0$ とすると、

　$M_0=\mu A\bar{D}$（$N\cdot m$）

そして、モーメントマグニチュードを $M_w$ とすると、

　$M_w={\displaystyle \frac{2}{3}{\log }_{10}{M}_0-10.7}$

マグニチュードには色々とある

地震波の測定方法によって使用されるものが異なります。

地震のタイプ、入手可能な情報、マグニチュードを使用する目的などにより、異なるマグニチュードスケールが使われます。

・実体波マグニチュード
・表面波マグニチュード
・気象庁マグニチュード

などが挙げられます。

東日本大震災のマグニチュードを計算

断層面の剛性率($\mu$)：$3.0\times {10}^{11}$($dyn/c{m}^2$)
断層面積の合計($c{m}^2$)：$(510\times {10}^5)\times (210\times {10}^5)$ ($c{m}^2$)
変位量の平均($cm$)：$12\times {10}^2$($cm$)

よって、

$M_0=3.0\times 510\times 210\times 12\times {10}^{23}$
　$=3.86\times {10}^{29}$

したがって、

$M_w={\displaystyle \frac{2}{3}{\log }_{10}(3.86\times {10}^{29})-10.7}$

　$={\displaystyle \frac{2}{3}({\log }_{10}3.86+{\log }_{10}{10}^{29})-10.7}$

　$={\displaystyle \frac{2}{3}(0.5866+29)-10.7}$
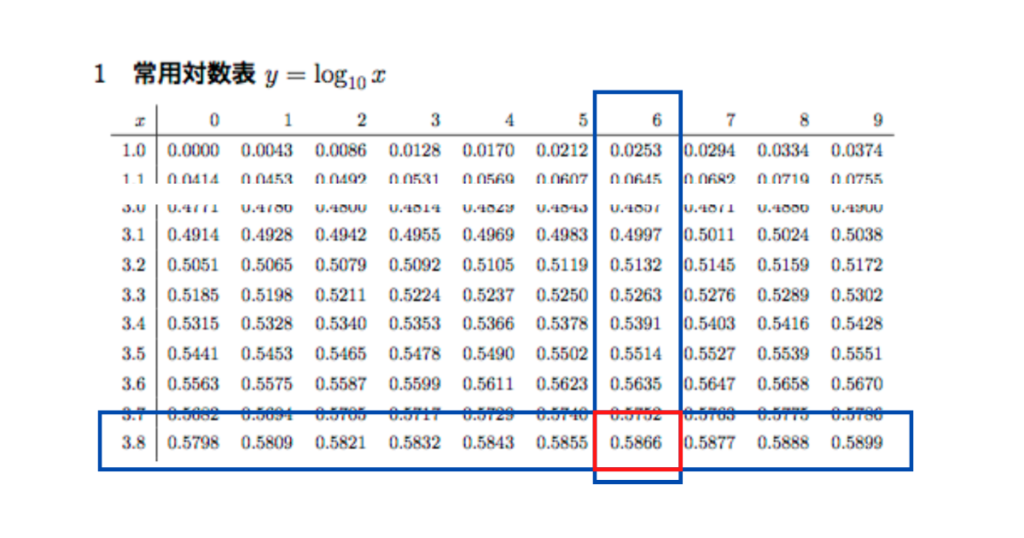
　（常用対数表を参照）

　$={\displaystyle \frac{2}{3}(29.5866)-10.7}$

　$=9.0244$

〈参考資料〉

国土交通省　気象庁　国内で発生した顕著な地震の震源課程解析結果

気象庁作成　平成23年(2011年)東北地方太平洋沖地震ー遠地実体波による震源課程解析（暫定）ー

地震被害と表層地盤の増幅特性　今岡克也　Slide 23

おわりに

改めてとなりますが、能登半島地震の被害に遭われた方には心よりお見舞い申し上げます。

今後も、記事を通して様々な情報を伝えていき、みなさんの何かの一助になれば嬉しいです。

また、本記事の「東日本大震災のマグニチュードの計算」部分について修正や追加情報等ございましたら遠慮なくコメントいただければ幸いです。

日本全体で乗り越えていきましょう！