集合の表し方
集合とは
集合とは、何らかの条件によって明確にグループ分けできる「もの」の集まりのことです。
例）全体集合 \(U\) を「乗り物」とする。
「乗り物」という集合には、乗用車、トラック、飛行機、 \(\cdots\) という要素が含まれます。
集合の表し方にはルールがあります。今回は、２パターンの表し方を例題を用いて解説していきます。
集合の表し方
① 要素を書き並べて表す。
\(A=\{2\), \(4\), \(6\), \(8\}\)
② 要素の満たす条件を述べて表す。
\(A=\{2n\) | \(n\) は整数, \(1\leq n\leq 4\}\)
どちらも同じ集合を表しています。①は要素を並べて表していますが、②は要素 \(n\) の説明を「|」の後にしています。①は \(1\), \(2\), \(3\) \(\cdots\) のように離散的な値に対して有効ですし、② は \(1\leq x \leq 4\) などの連続的な値に対して有効です。
集合の表し方（問題）
＞＞詳細はこちらから
集合の表し方の問題①
\(1\) から \(12\) までの自然数の集合を全体集合 \(U\) とし、その中で、 \(12\) の約数の集合を \(A\), \(8\) の約数の集合を \(B\) とするとき、次の集合を要素を書き並べて表せ。
(1) \(A\cap B\)
(2) \(\overline{A\cap B}\)
(3) \(\overline{A}\cup\overline{B}\)
(4) \(\overline{\overline{A}\cap B}\)
集合の表し方の問題②
\(-3<x<6\) を満たす整数 \(x\) の集合を全体集合 \(U\) とし、\(U\) の部分集合 \(A\), \(B\) を、
\(A=\{x\) | \(x\) は整数, \(0<x<5\}\)
\(B=\{x\) | \(x\) は整数, \(-2<x\leq 3\}\)
とするとき、次の集合を要素を書き並べて表せ。
(1) \(A\cap B\)
(2) \(A\cup B\)
(3) \(\overline{A}\)
(4) \(\overline{B}\)
(5) \(\overline{A}\cap B\)
集合の表し方（解説）
集合の表し方の問題（解説）①
ベン図で表しておくと解きやすくなります！
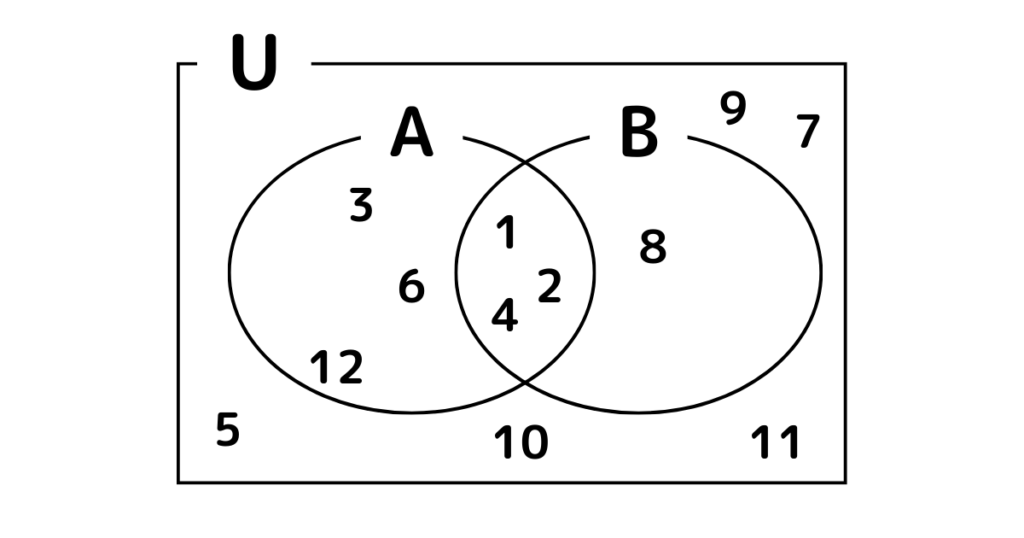
(1) \(A\cap B\)
\(A\cap B=\{1,\ 2,\ 4\}\)
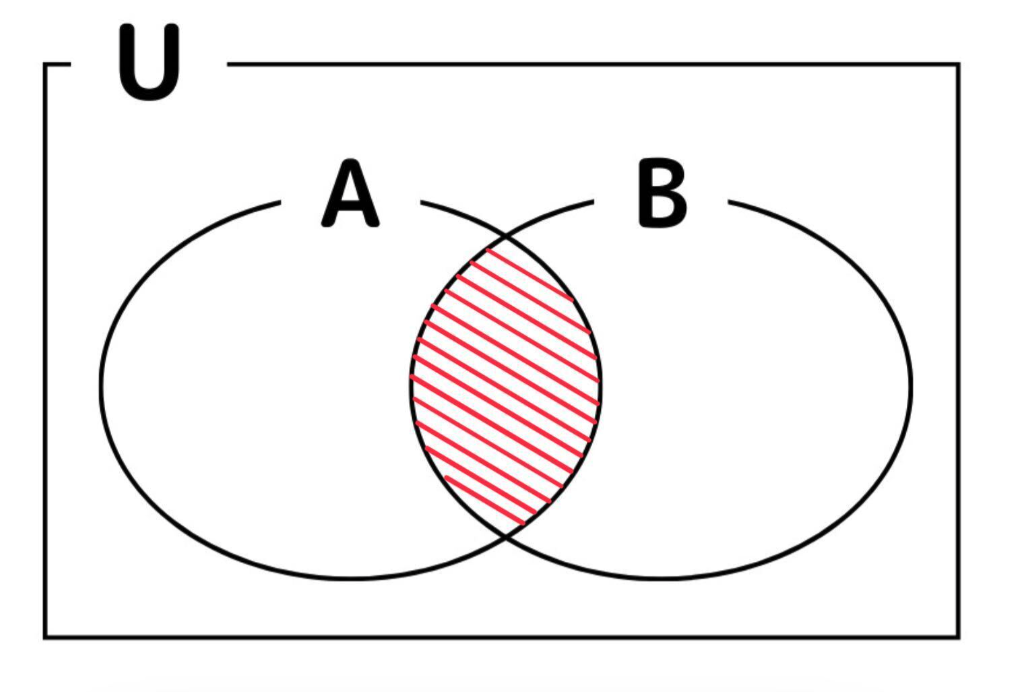
(2) \(\overline{A\cap B}\)
(1) より \(A\cap B=\{1,\ 2,\ 4\}\)
よって、
\(\overline{A\cap B}=\{3,\ 5,\ 6,\ 7,\ 8,\ 9,\ 10,\ 11,\ 12\}\)
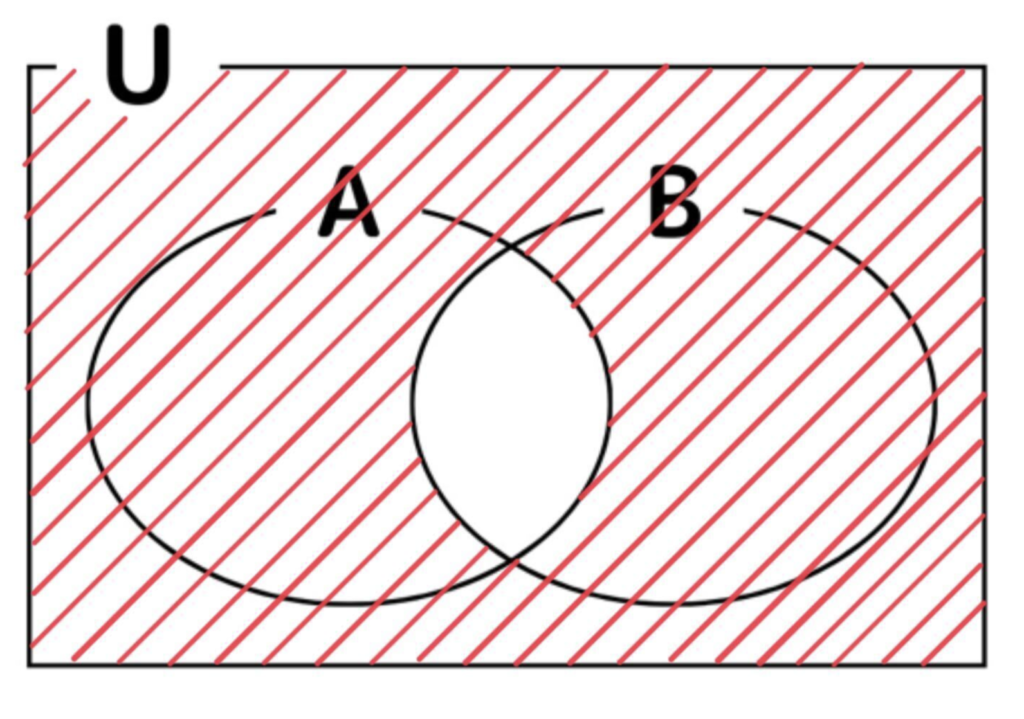
(3) \(\overline{A}\cup\overline{B}\)
ド・モルガンの法則より
\(\overline{A}\cup\overline{B}=\overline{A\cap B}\)
\(\overline{A\cap B}=\{3,\ 5,\ 6,\ 7,\ 8,\ 9,\ 10,\ 11,\ 12\}\)
(4) \(\overline{\overline{A}\cap B}\)
(2) より
\(\overline{A}\cap B=\{8\}\)
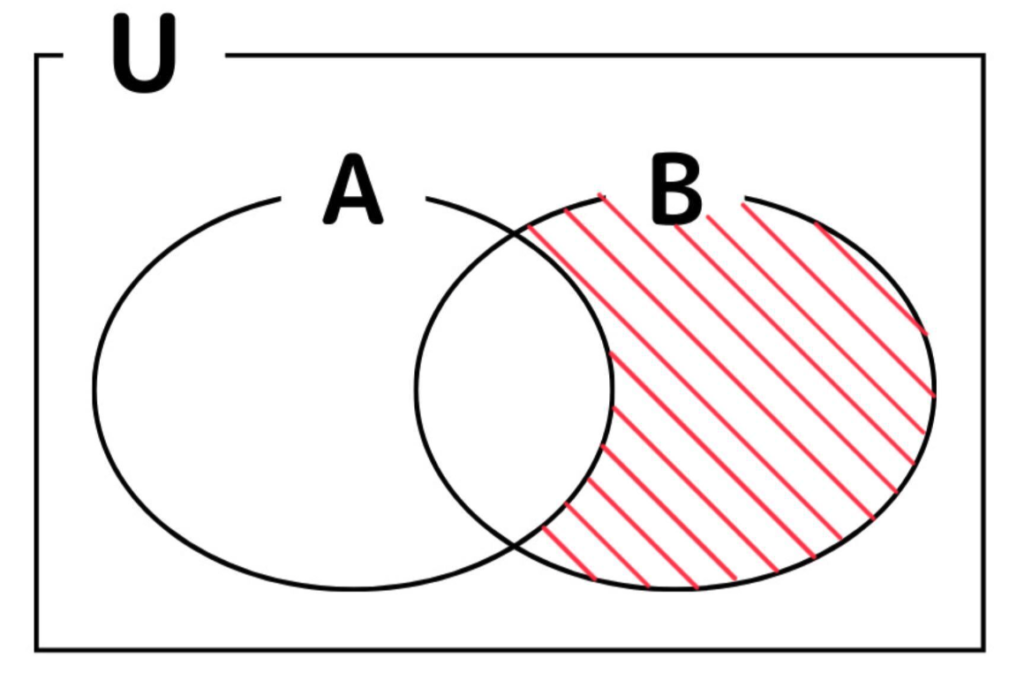
よって、
\(\overline{\overline{A}\cap B}=\{1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 9,\ 10,\ 11,\ 12\}\)
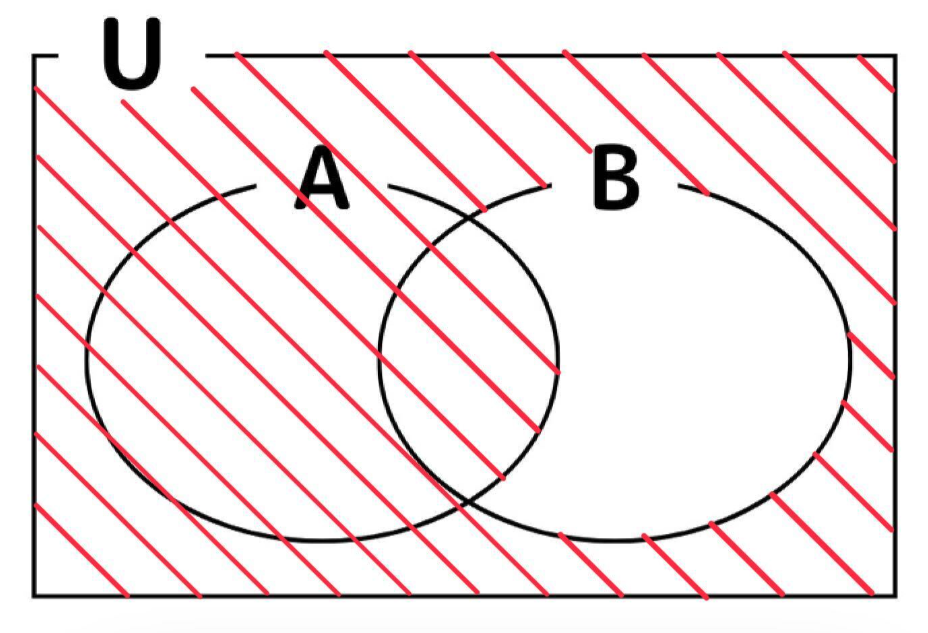
集合の表し方の問題（解説）②
今回の集合の表し方は、ベン図で表すことが出来ません。
そんな時は、数直線上で表す。
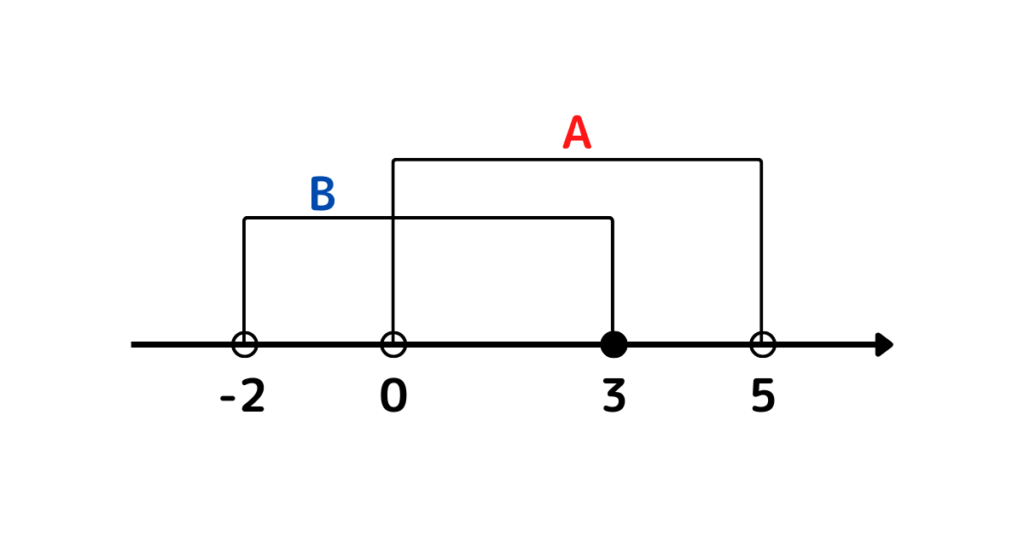
(1) \(A\cap B\)
\(A\cap B=\{x\) | \(x\) は整数, \(0<x\leq 3\}\)
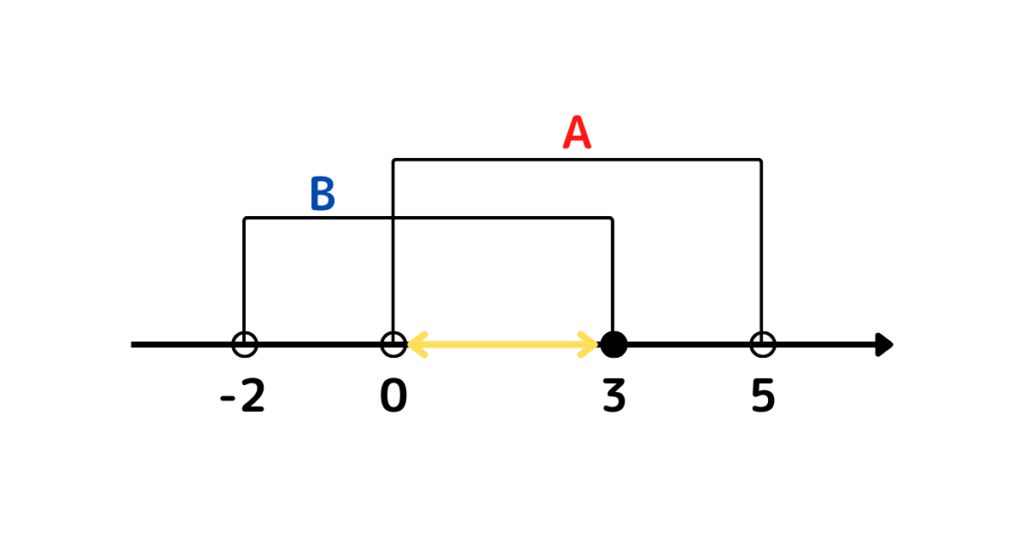
(2) \(A\cup B\)
\(A\cup B=\{x\) | \(x\) は整数, \(-2<x<5\}\)
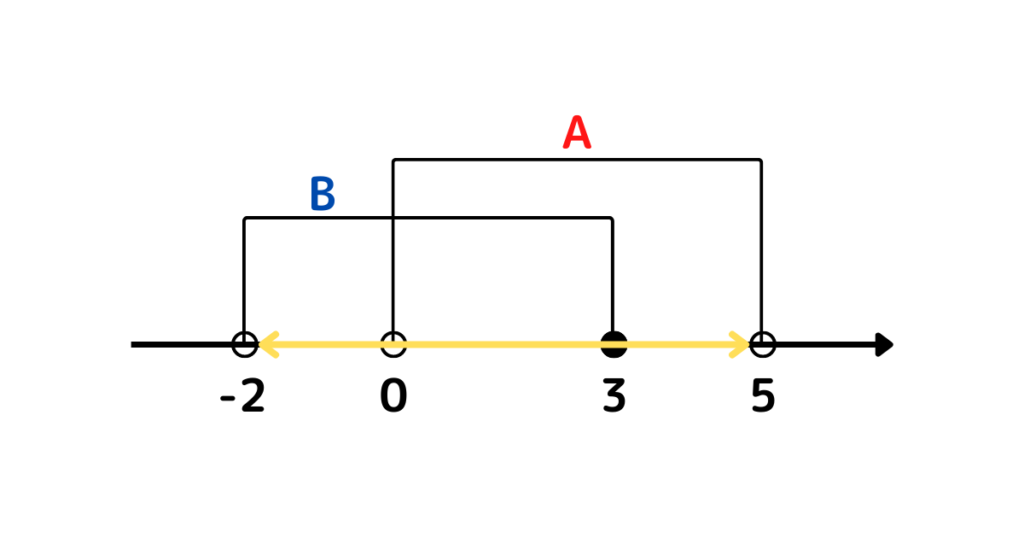
(3) \(\overline{A}\)
\(\overline{A}=\{x\) | \(x\) は整数 \(x<0\), \(5<x\}\)
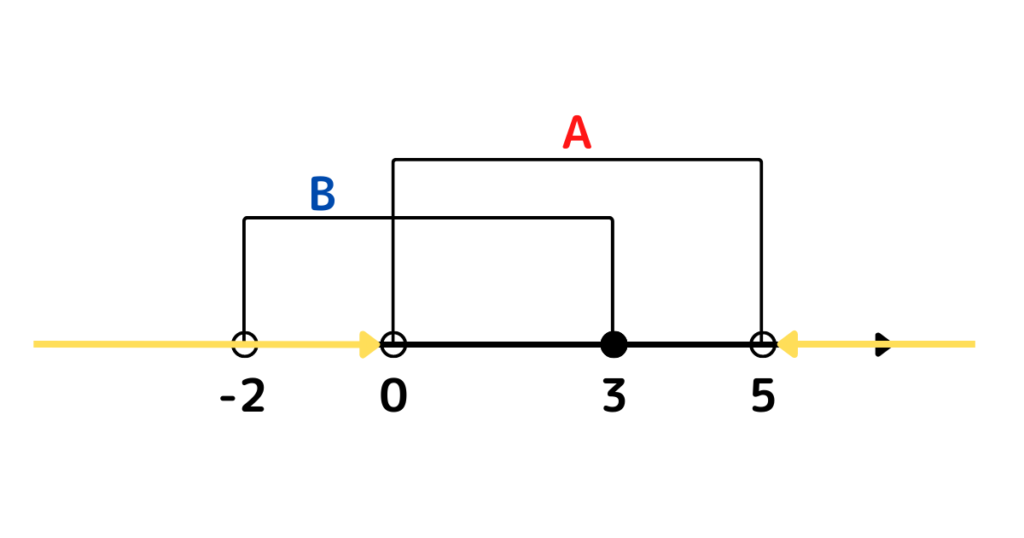
(4) \(\overline{B}\)
\(\overline{B}=\{x\) | \(x\) は整数 \(x<-2\), \(3\leq x\}\)
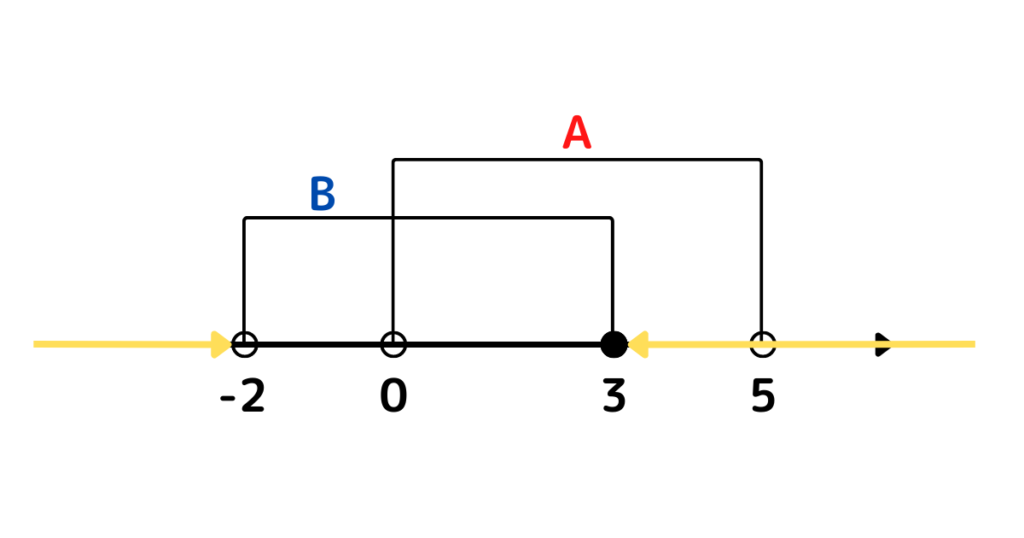
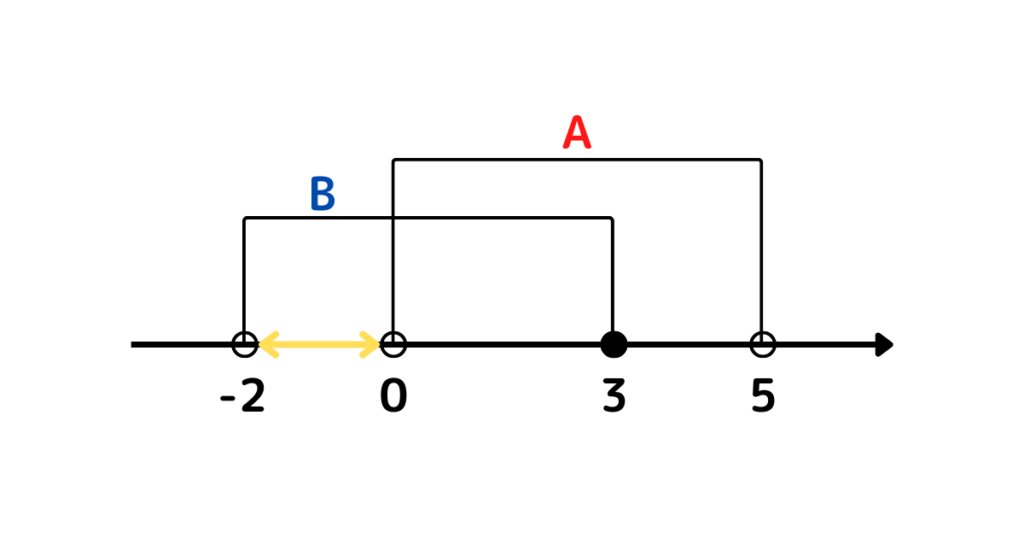
(5) \(\overline{A}\cap B\)
\(\overline{A}\cap B=\{x\) | \(x\) は整数 \(-2<x<0\}\)
おわりに
さいごまで読んでいただきありがとうございました！
【最新】こちらの記事がおすすめ！