十分条件と必要条件
十分条件と必要条件の定義
十分条件と必要条件の定義
\(2\) つの条件 \(p\) と \(q\) において、「\(p\) ならば \(q\)」が成り立つ（真である）とき、
\(p\) は \(q\) であるための必要条件である
\(q\) は \(p\) であるたのの十分条件である
十分条件と必要条件の例
例1）
「リンゴならば果物である」
真偽の確認：リンゴはどんな時でも果物なので、「リンゴならば果物である」は真で成り立ちます。
このとき、
果物はリンゴの必要条件である
リンゴは果物の十分条件である
となります。
「果物ならばリンゴである」
真偽の確認：果物の中には、梨やみかんなどリンゴ以外にも様々ありますので、偽で成り立ちません。
例２）
「東京都民ならば日本国民である」
真偽の確認：東京都民を一人ずつ調べると全員日本国民であるので、「東京都民ならば日本国民である」は真で成り立ちます。
このとき、
東京都民は日本国民の必要条件である
日本国民は東京都民の十分条件である
となります。
「日本国民ならば東京都民である」
真偽の確認：日本国民の中には、他の都道府県の人たちも混じってるので、偽で成り立ちません。
必要条件は、大きく包括してる方、十分条件は、小さく限定的なもの。このようにイメージするとわかりやすいと思います！
ここまでの内容で、真とか偽など用語の意味が全然わからない方は一度こちらの記事をチェックしてみてください
＞＞詳細はこちらから
十分条件と必要条件の覚え方
例題①）「リンゴは果物であるための◯◯条件」
例題②）「\(x^2=4\) は \(x=2\) であるための◯◯条件」
十分条件と必要条件の覚え方「言葉の意味で覚える」
「\(\spadesuit\) \(\spadesuit\) は \(\clubsuit\) \(\clubsuit\) であるための◯◯条件」
例題①）「リンゴは果物であるための◯◯条件」
解説①）
リンゴであれば果物であることが十分に言えるので、答えは十分条件
例題②）「\(x^2=4\) は \(x=2\) であるための◯◯条件」
解説②）
\(x^2=4\) だけだと、\(x=2\) であることは言えません。\(x=2\) であることを言うためには他に条件が必要です。
よって、\(x^2=4\) は \(x=2\) であることを成り立たせるための必要な条件の一つであるので、答えは必要条件
十分条件と必要条件の覚え方「矢印の向きで覚える」
「\(\spadesuit\) \(\spadesuit\) は \(\clubsuit\) \(\clubsuit\) であるための◯◯条件」
例題①）「リンゴは果物であるための◯◯条件」
解説①）
「リンゴならば果物」は真
「果物ならばリンゴ」は偽
よって、答えは十分条件
例題②）「\(x^2=4\) は \(x=2\) であるための◯◯条件」
解説②）
「\(x^2=4\) ならば \(x=2\)」は偽
「\(x=2\) ならば \(x^2=4\)」は真
よって、答えは必要条件
十分条件と必要条件の覚え方「ベン図で覚える」
ベン図で表す方法を紹介します。
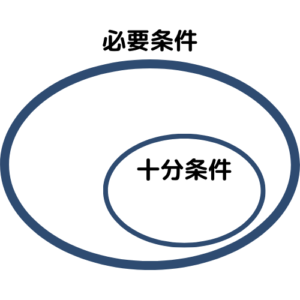
外側の円、つまり大きく広いほうが必要条件です。「広いの“ひ”は必要の“ひ”」と覚えるのもいいですね。
例題①）「リンゴは果物であるための◯◯条件」
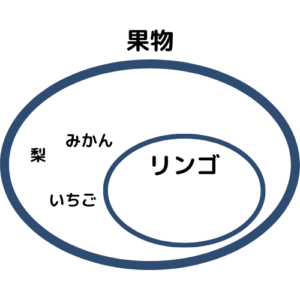
よって、リンゴは十分条件
例題②）「\(x^2=4\) は \(x=2\) であるための◯◯条件」
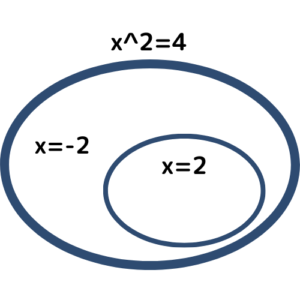
よって、\(x^2=4\) は必要条件
おわりに
十分条件と必要条件の説明をしてきました。
問題の解き方は３種類あり、
- 言葉の意味で覚える
- 矢印の向きで覚える
- ベン図で覚える
さいごまで読んでいただきありがとうございました！
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学（統計検定）の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。（Xはこちら）
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。
質問や感想はコメントへ！