二次不等式の解き方
二次不等式とは、以下の例のような形の式です。
例)
① \(x^2+3x+2>0\)
② \(x^2+4x<0\)
グラフを描いて二次不等式を解く
\(ax^2+bx+c=0\) の解を \(x=\alpha\), \(\beta\) とする。このとき、
\(ax^2+bx+c>0\)
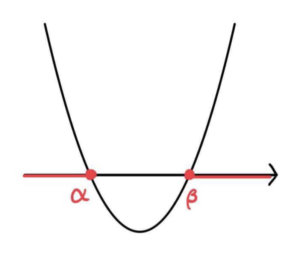
グラフより、\(x<\alpha\), \(\beta<x\)
\(ax^2+bx+c<0\)
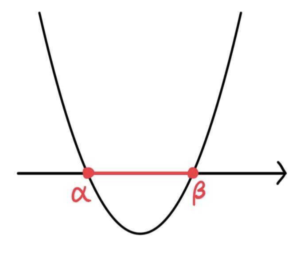
グラフより、\(\alpha<x<\beta\)
例題)
① \(x^2+3x+2>0\)
\(x^2+3x+2=(x+2)(x+1)>0\)
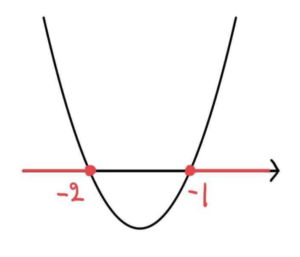
グラフより、\(x<-2\), \(-1<x\)
② \(x^2+4x<0\)
\(x(x+4)<0\)
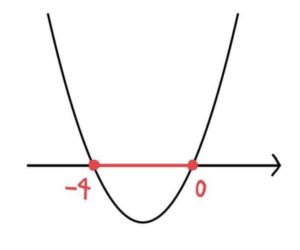
グラフより、\(-4<x<0\)
因数分解を用いて二次不等式を解く
\(a<b\) とすると、
\((x-a)(x-b)>0\) → \(x<a\), \(b<x\)
\((x-a)(x-b)<0\) → \(a<x<b\)
例題)
① \(x^2+3x+2>0\)
\(x^2+3x+2=(x+2)(x+1)>0\)
\(x<-2\), \(-1<x\)
② \(x^2+4x<0\)
\(x(x+4)<0\)
\(-4<x<0\)
少し難しい二次不等式の問題
解の公式が必要な二次不等式
例題)\(x^2-6x+7\leq 0\)
\(x^2-6x+7=0\)を解くと、\(x=3\pm\sqrt{2}\) となるので、
\(3-\sqrt{2}<x<3+\sqrt{2}\)
解が存在しない二次不等式
例題)\(x^2+2x+4\leq 0\)
これまでの問題と違う部分
\(x^2+2x+4=0\) にしてみると、これを満たす解が存在しないことがわかります。
判別式 \(D\) を計算してみると、\(D=4-16=-12\) となり、実数解を持たないことがわかります。

グラフを描いてみると、
\(x^2+2x+4=(x+1)^2+3\) となるので、下図のようになります。
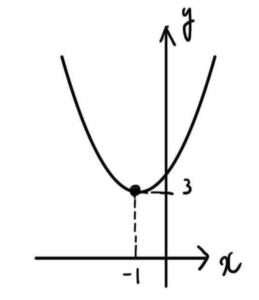
よって、すべての実数 \(x\) で \(x^2+2x+4\) が \(0\) 以上になることがわかります。
まとめ
二次不等式は、
① 因数分解することにより解く
② グラフを描くことにより解く
この2つの方法を駆使しながら解くと良いでしょう。しかし、①のように必ずしも因数分解ができるわけではありませんので、②のようにグラフを描く方法もできるようにしておきましょう。記事の内容でよくわからないところがありましたら、下記のお問い合わせフォームよりご連絡ください。
さいごまで読んでいただきありがとうございました!
【最新】こちらの記事がおすすめ!




