逆と裏は同じ?混乱するポイントを解説
今回は命題の分野で見かけるワードである、「逆」、「裏」、「対偶」について解説していきます!
逆と裏がどっちがどっちか混乱するポイントですね…
具体的な問題でこれらを解説していきますので、最後まで見てみてください!
【対偶への変換方法】

元の命題を”裏”にしてから”逆”に、もしくは”逆”にしてから”裏”にします!
〈元の命題〉
積 \(ab\)が \(3\)の倍数ならば \(a\) または \(b\) は \(3\) の倍数である。
〈逆〉※「ならば」の両側を入れ替える。
\(a\) または \(b\) は \(3\) の倍数である。ならば、積 \(ab\) が \(3\) の倍数である。
〈裏〉※「ならば」の両側を否定する。
積 \(ab\) が \(3\) の倍数ではない。ならば \(a\) または \(b\) は \(3\) の倍数ではない。
〈対偶〉※”逆(裏)” をしてから ”裏(逆)”をする。
\(a\) かつ \(b\) は \(3\) の倍数ではない。ならば、積 \(ab\) は \(3\) の倍数ではない。
逆・裏・対偶(問題)
命題「自然数 \(a\) 、 \(b\) について、 \(a^2+b^2\) が奇数ならば \(ab\) は偶数である」が与えられている。
(\(1\))与えられた命題の裏を答えなさい。
(\(2\))与えられた命題の対偶を答えなさい。
(\(3\))対偶を用いて、与えられた命題が成り立つかどうかを調べなさい。
>>詳細はこちらから
答案の例
(\(1\)) 与えられた命題の裏を答えなさい。
「自然数 \(a\) 、 \(b\) について、 \(a^2+b^2\) が偶数ならば \(ab\) は奇数である」
(\(2\)) 与えられた命題の対偶を答えなさい。
「自然数 \(a\) 、 \(b\) について、 \(ab\) が奇数ならば \(a^2+b^2\) は偶数である」
(\(3\)) 対偶を用いて、与えられた命題が成り立つかどうかを調べなさい。
\(ab\) が奇数ならば、 \(a\) 、 \(b\) はともに奇数であり、
\(a=2m+1\)
\(b=2n+1\)
(\(m\)、\(n\) は \(0\) 以上の整数)
とおける。このとき、
\(a^2+b^2=(2m+1)^2+(2n+1)^2\)
\(=(4m^2+4m+1)+(4n^2+4n+1)\)
\(=2(2m^2+2n^2+2m+2n+1)\)
\(2m^2+2n^2+2m+2n+1\) は整数であるから、 \(a^2+b^2\) は偶数である。
よって、命題の対偶は真となる。
つまり、与えられた命題も成り立つ。
解説
(\(1\)) 与えられた命題の裏を答えなさい。
基本的な考え方は、上記の解答を見れば、わかると思います。
日常会話でも、「裏を返せば、~」という表現を使ったことがある人も多いのではないでしょうか?
例えば、「顔はイケメンだよね」と言われたら、男性のみなさんはおそらく、
「裏を返せば、顔以外はイケメンじゃないってことね」と捉えませんか?
つまり「裏」とは、文章の意味をひっくり返すことを指しています。
また、「イケメンである」という文章を、「イケメンではない」というように否定する形で意味をひっくり返していますね。
よって、この「文章の意味をひっくり返す」という表現を、数学では「あることがらを否定する」と言います。
ちなみに復習ですが、「逆」とは、
「AならばB」 \(\longrightarrow\) 「BならばA」
のように、言葉の前後をひっくり返すことを指していましたね。
「逆」・・・言葉の前後をひっくり返す
「裏」・・・文章の意味をひっくり返す
というわけで、今回は
「 \(a^2+b^2\) が奇数ならば \(ab\) は偶数である」
の裏を答えるので、この文章の意味をひっくり返し、
「 \(a^2+b^2\) が偶数ならば \(ab\) は奇数である」
ということになるのです。
また、「自然数 \(a\) 、 \(b\) について」というのは本題に入る前の、前置きのようなものなので、この部分はひっくり返す必要はありません。
ちなみに、逆のときと同様、裏についても、成り立つかどうかはわかりません。
今回は裏を答えるだけなので、この命題を確かめることはしないでおきます。
(\(2\)) 与えられた命題の対偶を答えなさい。
「対偶」とは、「逆」と「裏」を組み合わせたものを言います。
よって、(\(1\))の
「\(a^2+b^2\) が偶数ならば \(ab\) は奇数である」
ということがらの逆を言えば、対偶にあたります。
つまり、「 \(ab\) が奇数ならば \(a^2+b^2\) は偶数である」となります。
(\(3\)) 対偶を用いて、与えられた命題が成り立つかどうかを調べなさい。
まず、「与えられた命題」と「対偶」が、どのように関係しているかを説明します。
「PならばQ」という命題があったとき、図でその状況を考えてみます。
まずは、元の命題が真であるとき、対偶の真偽がどうなるかを検証してみましょう。
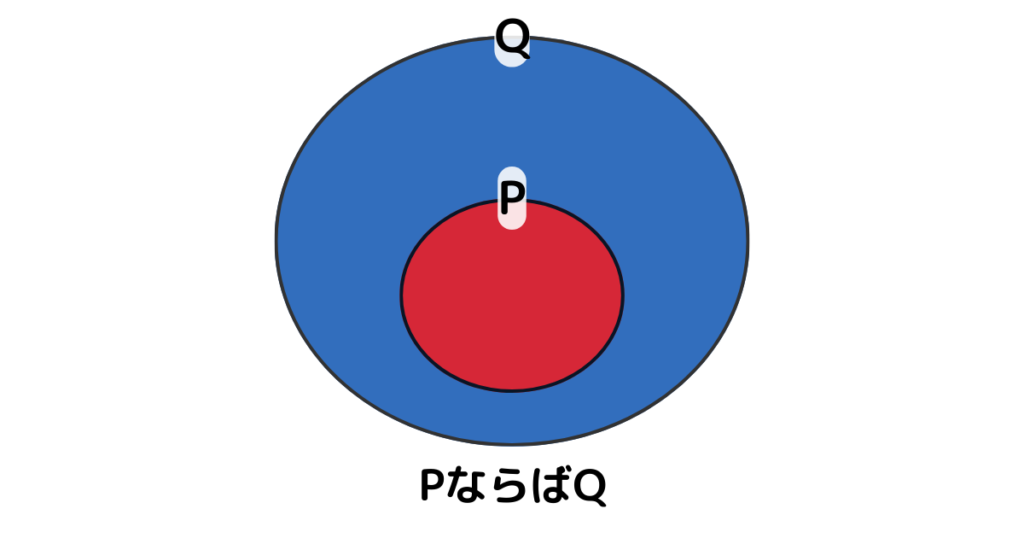

図 \(1\) のように、Pが成り立つときは、赤い部分が成り立っているということですね。
そのとき、Q(青い部分)は完全に赤い部分とかぶっているので、これは元の命題が真であるパターンの一例であるわけです。
続いて、その対偶にあたる「QでないならばPでない」という命題を考えてみます。
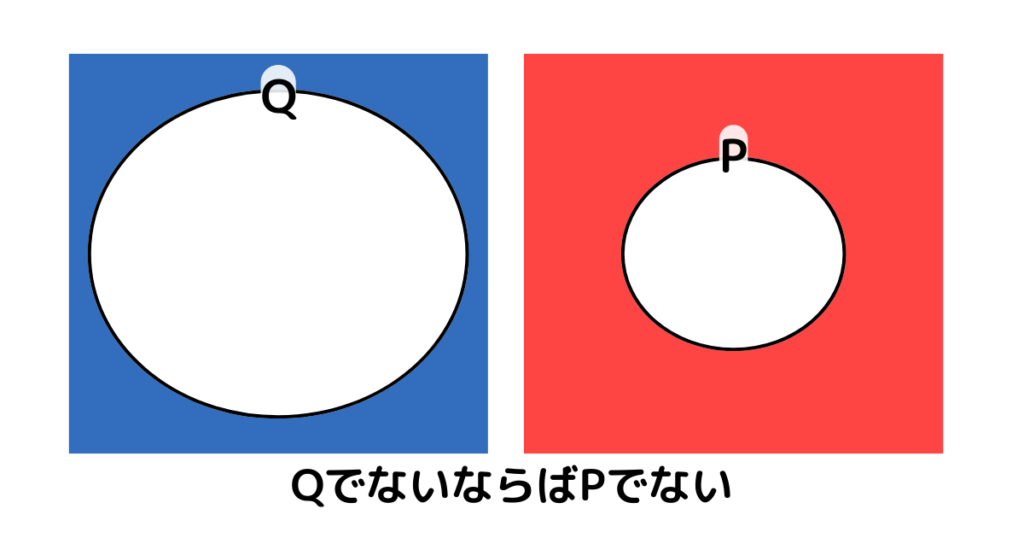

図 \(2\)のQでない部分(青い部分)はPでない部分(赤い部分)と完全にかぶっています。よって、こちらの命題も真ということになります。
※四角は全体集合を表しています。
これにより、元の命題が真のとき、その対偶は真になるという結果となりました。
では、元の命題が偽になる場合はどうなのでしょう?
「PならばQ」が成り立たない場合、例えば図 \(3\) のようになっています。
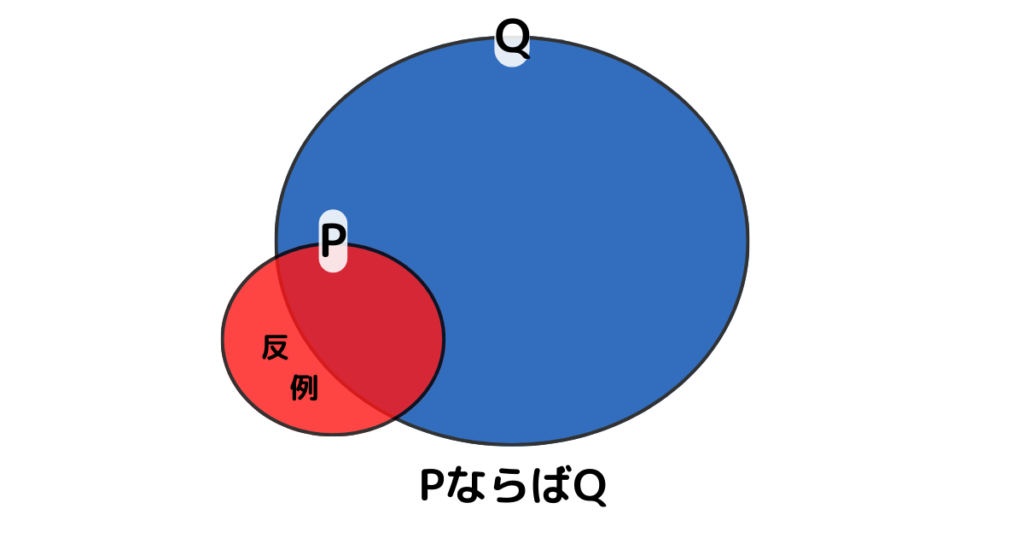

Pが成り立つ場合、赤い部分が成り立っているので、Qの青い部分ににかぶっていれば良いのですが、はみ出してしまっていますね。
よって、はみ出し部分が反例となり、成り立たない、つまりは偽ということになります。
この対偶も、同様に反例が邪魔をして偽となってしまいます。
よって、元の命題が偽のとき、その対偶も偽になるという結果となりました。
細かい証明は省きますが、以上のことから、元の命題とその対偶の真偽は一致することがわかります。
この性質を利用し、元の命題の真偽が証明しにくい場合、対偶の真偽を証明する方向に切り替えるのです。
① 対偶が真であるとき、元の命題は真
② 対偶が偽であるとき、元の命題は偽
さて、では実際に、( \(2\) )で求めた対偶の真偽を確かめてみましょう。
\(ab\) は奇数であるという前提がありますので、積が奇数になるのは、
「奇数×奇数」
の組み合わせしかありません。よって、 \(a\) も \(b\) も奇数ということです。
さらに、 \(a^2\) や \(b^2\) は、同じく「奇数×奇数」を表しているため、どちらも奇数となりますね。
そして、その和である「 \(a^2+b^2\) 」は、「奇数+奇数」なので、偶数となります。
これを数学的に説明すれば、証明完了です。
まず、 \(a\) 、 \(b\) はともに奇数なので、
\(a=2m+1\)
\(b=2n+1\)
(\(m\)、\(n\) は \(0\) 以上の整数)
とおけます。このとき、
\(a^2+b^2\)
\(=(2m+1)^2+(2n+1)^2\)
\(=(4m^2+4m+1)+(4n^2+4n+1)\)
\(=2(2m^2+2n^2+2m+2n+1)\)
ここで、\(m\)と\(n\) は \(0\) 以上の整数と限定されているので、\(2m^2+2n^2+2m+2n+1\) も整数となります。
よって、 \(a^2+b^2\) は偶数になるというわけです。
以上のことから、対偶である「 \(ab\) が奇数ならば \(a^2+b^2\) は偶数である」ということがらは、真ということになります。
よって、上記のポイントに従い、元の命題も真となるのです。
大抵の場合、「AならばB」という命題において、Aの部分が理解しやすいとき、その命題の真偽を判定しやすいです。
今回は、元の命題において、 「\(a^2+b^2\) が奇数」というのは少し理解しにくいですね。
そのため、対偶を利用し、Aの部分をわかりやすくしたのです。
おわりに
さいごまで読んでいただきありがとうございました!
【最新】こちらの記事がおすすめ!





