【図形と方程式】『軌跡』アポロニウスの円の例題とその解説

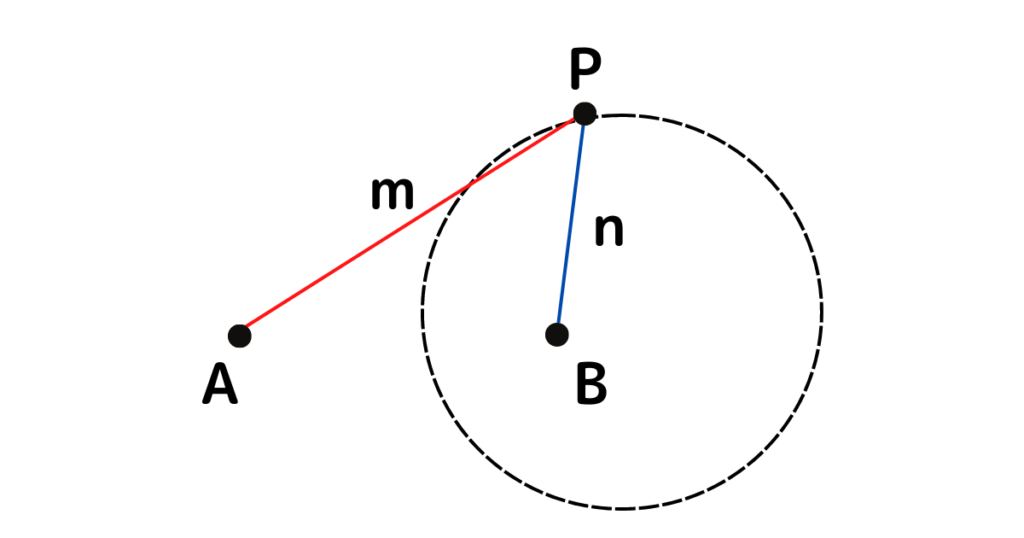
シンプルな条件からできるシンプルな図形、これが数学の美しさ

by yu-to

アポロニウスの円

今回は軌跡の問題を解説します！

高校数学で学習する『軌跡』で一番最初に登場する軌跡問題が『アポロニウスの円』です。

軌跡問題は決まった数式や公式があるわけではないので苦手な人が多いのですが、解く手順は存在します。例題に入る前に解き方の手順を確認していきましょう！

アポロニウスの円とは？

軌跡問題の解法

①　動点の見極め
問題文を図示した上で、どの点が動く点なのかを考えましょう！

②　動点を 点 $P(x$,　$y)$ と置く
方程式からどんなグラフなのかを見極めるので $x$ と $y$ で表すのが一般的です。

③　$x$ と $y$ を用いた方程式を立てる
１番の難所ですが問題文のどこかに方程式を立てるための条件が隠されています。例えば、最終的な式が一次式なら直線になりますし、二次式なら円になります。

アポロニウスの円（問題）

$2$ 点 $A(-4$,　$0)$,　 $B(2$,　$0)$ からの距離の比が $2:1$ である点の軌跡を求めよ。

答案の例

条件を満たす点を $P(x$,　$y)$ と置く。

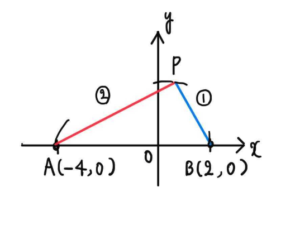
図より、$AP:BP=2:1$

ゆえに、$AP=2BP$

両辺を $2$ 乗すると、$A{P}^2=4B{P}^2$ $\cdots$ ※

となる。よって、$(x+4{)}^2+y^2=4(x-2{)}^2+y^2$

整理すると、$x^2+8x+16+y^2=4(x^2-4x+4+y^2)$

$$\begin{array}{rcl}{x}^2+8x+16+y^2& =& 4x^2-16x+16+4y^2\\ -3x^2+24x-3y^2& =& 0\\ x^2-8x+y^2& =& 0\\ (x-4{)}^2+y^2& =& 16\end{array}$$

よって、条件を満たす点は、円 $(x-4{)}^2+y^2=16$ 上にある。

逆に、円 $(x-4{)}^2+y^2=16$ 上の任意の点は、条件を満たす。

したがって問題を満たす軌跡は、

中心が $(4$,　$0)$,　半径が $4$ の円

解説

今回の場合は、点 $A$,　点 $B$ からの距離の比が $2:1$ である点が動点となる。よって、そのような条件を満たす点を $P(x$,　$y)$ と置く。

図より、$AP:BP=2:1$

ゆえに、$AP=2BP$

両辺を $2$ 乗すると、$A{P}^2=4B{P}^2$ $\cdots$ ※

となる。

$A{P}^2$ と $B{P}^2$ をそれぞれ求める

　$A{P}^2$ について

　　点 $A(-4$,　$0)$,　点 $P(x$,　$y)$ より

　　$A{P}^2=(x+4{)}^2+y^2$

　$B{P}^2$ について

　　点 $B(2$,　$0)$,　点 $P(x$,　$y)$ より

　　$B{P}^2=(x-2{)}^2+y^2$

それぞれ ※ に当てはめると、

　$(x+4{)}^2+y^2=4(x-2{)}^2+y^2$

整理すると、

$$\begin{array}{rcl}{x}^2+8x+16+y^2& =& 4x^2-16x+16+4y^2\\ -3x^2+24x-3y^2& =& 0\\ x^2-8x+y^2& =& 0\\ (x-4{)}^2+y^2& =& 16\cdots \mathrm{①}\end{array}$$

動点として置いた、点 $(x$,　$y)$ を用いた方程式が出来たので、条件を満たす点は、

円 $(x-4{)}^2+y^2=16$ 上にある。

逆に、円 $(x-4{)}^2+y^2=16$ 上の任意の点は、条件を満たす。

「逆に、」の部分は、必要十分条件を満たすことを確認するために必要な作業ですが、大学入試によっては、自明だから必要としない大学もあるため、深く考える必要はありません。機械的に書ければ良いです。

したがって問題を満たす軌跡は、中心が $(4$,　$0)$,　半径が $4$ の円 $\cdots$ A

「軌跡の方程式を求めよ」なら、答えは ① のままでよいのですが、「軌跡を求めよ」の場合は、A のように答えに図形の形を示す必要があるので注意しましょう！

おわりに

今回は、軌跡の問題を解説しました。

今回のように 解法に当てはめる 癖もつけましょう。