【数列】『漸化式』漸化式を用いた確率の解法

確率と漸化式

さいころを複数回投げる時、\(1\) の目が \(2\) 回出る確率を求めたいとすると、

\(2\) 回投げる時に \(1\) の目が \(2\) 回出る確率 → \(p_2\) と表す。
\(5\) 回投げる時に \(1\) の目が \(2\) 回出る確率 → \(p_5\) と表す。
\(n\) 回投げる時に \(1\) の目が \(2\) 回出る確率 → \(p_n\) と表す。

「さいころを複数回投げる時」のように、果てしなく続く場合は、このように表すと便利です。

漸化式とは

漸化式とは、\(n\) 回目の値と \(n+1\) 番目の値の関係性

今回の例なら、さいころを \(n\) 回投げて、\(1\) の目が \(2\) 回出る確率（値）を、\(p_n\)、さいころを \(n+1\) 回投げて、\(1\) の目が \(2\) 回出る確率（値）を、\(p_{n+1}\) とおくとき、

\(p_n\) と \(p_{n+1}\) の関係性を表すとそれが漸化式となる。

漸化式の全パターン

数列の基礎基本はこちら

漸化式の問題

さいころを \(n\) 回投げる時、\(1\) の目が偶数回出る確率を \(p_n\) とする。ただし、\(0\) は偶数と考える。このとき、\(p_n\) と \(p_{n+1}\) の間に成り立つ関係式を求めなさい。

漸化式の問題（答案の例）

さいころを \((n+1)\) 回投げるとき、\(1\) の目が偶数回出る確率 \(p_{n+1}\) について \(p_{n+1}\) は、

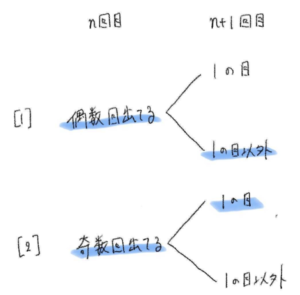
[1]　\(n\) 回目までに \(1\) の目が偶数回出て、\((n+1)\) 回目に \(1\) 以外の目が出る確率
[2]　\(n\) 回目までに \(1\) の目が奇数回出て、\((n+1)\) 回目に \(1\) の目が出る確率

の和で求めることができます。

[1] の確率は、\(p_n\cdot \displaystyle\frac{5}{6}\) \(\cdots\) ①

[2] の確率は、\((1-p_n)\cdot \displaystyle\frac{1}{6}\) \(\cdots\) ②

①、② より

\(p_{n+1}=p_n\cdot \displaystyle\frac{5}{6}+(1-p_n)\cdot\displaystyle\frac{1}{6}\)
\(p_{n+1}=\displaystyle\frac{5}{6}p_n+\displaystyle\frac{1}{6}\)

漸化式の問題（解説）

[1] の確率

\(n\) 回目までに \(1\) の目が偶数回出る確率は、\(p_n\)
\(n+1\) 回目に \(1\) 以外の目が出る確率は、\(\displaystyle\frac{5}{6}\)

よって、\(p_n\cdot \displaystyle\frac{5}{6}\) \(\cdots\) ①

[2] の確率

\(n\) 回目までに \(1\) の目が奇数回出る確率は、\(1-p_n\)

\(1\) の目が偶数回出る確率：\(p_n\)
\(1\) の目が奇数回出る確率：\(q_n\) とおくと

\(p_n+q_n=1\)
\(q_n=1-p_n\)

と表すことができる。\(n+1\) 回目に \(1\) の目が出る確率は、\(\displaystyle\frac{1}{6}\)

よって、\((1-p_n)\cdot \displaystyle\frac{1}{6}\) \(\cdots\) ②

①、② より

\(p_{n+1}=p_n\cdot \displaystyle\frac{5}{6}+(1-p_n)\cdot \displaystyle\frac{1}{6}\)
\(p_{n+1}=\displaystyle\frac{5}{6}p_n+\displaystyle\frac{1}{6}\)

おわりに

今回は、確率と漸化式が組み合わさった問題でした。