円順列とじゅず順列の違い
今回は、円順列とじゅず順列について例題を交えながら解説していきます。
順列
異なる \(n\) 個のものの中から異なる \(r\) 個を選んで並べる。
その時の順列の総数は、\({}_nP_r=n\times (n-1)\times (n-2)\cdots (n-r+1)\)
円順列
いくつかのものを円形に並べる配列を円順列という。
円順列では、適当に回転して並びが一致するものは同じものとして考えるので、
\(\displaystyle\frac{{}_nP_n}{n}=(n-1)!\) となる。
じゅず順列
異なるいくつかのものを円形に並べ、回転または裏返して一致するものは同じものとみるとき、その並び方をじゅず順列という。
円順列の並び方の中には、裏返し一致するものが \(2\) つずつあり、
じゅず順列の総数は円順列の総数の半分なので、\(\displaystyle\frac{(n-1)!}{2}\) となる。
順列と円順列とじゅず順列の違い
順列と円順列
\(A\), \(B\), \(C\), \(D\) を 1 列に並べる順列を考える。
\(A\) \(B\) \(C\) \(D\)
\(B\) \(C\) \(D\) \(A\)
\(C\) \(D\) \(A\) \(B\)
\(D\) \(A\) \(B\) \(C\)
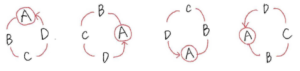
このように、\(1\) 列で並べると \(4\) 種類に分かれるものでも円状に並べてみると、同じ並び方になります。
※ 右回りもしくは左回りに回転させると同じ並び方になります。
順列と円順列
\(A\), \(B\), \(C\), \(D\) を 1 列に並べる順列を考える。
\(A\) \(B\) \(C\) \(D\)
\(B\) \(C\) \(D\) \(A\)
\(C\) \(D\) \(A\) \(B\)
\(D\) \(A\) \(B\) \(C\)
このように、\(1\) 列で並べると \(4\) 種類に分かれるものでも円状に並べてみると、同じ並び方になります。
※ 右回りもしくは左回りに回転させると同じ並び方になります。
円順列とじゅず順列の問題
異なる 6 個の宝石がある。
(1) これらの宝石を \(1\) 列に並べる方法は何通りあるか。
(2) これらの宝石を机の上で円形に並べる方法は何通りあるか。
(3) これらの宝石で首飾りを作るとき、何種類の首飾りができるか。
円順列とじゅず順列（解説）
(1) これらの宝石を \(1\) 列に並べる方法は何通りあるか。
\(6!=6\times 5\times 4\times 3\times 2\times 1=720\)
(2) これらの宝石を机の上で円形に並べる方法は何通りあるか。
6 個の宝石を机の上で円形に並べる方法は、\(\displaystyle\frac{{}_6C_6}{6}=(6-1)!=5!=120\)
(3) これらの宝石で首飾りを作るとき、何種類の首飾りができるか。
(1) の並べ方のうち、裏返して一致するものを同じものと考えるので、\(\displaystyle\frac{(6-1)!}{2}=\frac{5!}{2}=60\)
おわりに
円順列
いくつかのものを円形に並べる配列を円順列という。
円順列では、適当に回転して並びが一致するものは同じものとして考えるので、
\(\displaystyle\frac{{}_nP_n}{n}=(n-1)!\) となる。
じゅず順列
異なるいくつかのものを円形に並べ、回転または裏返して一致するものは同じものとみるとき、その並び方をじゅず順列という。
円順列の並び方の中には、裏返し一致するものが \(2\) つずつあり、
じゅず順列の総数は円順列の総数の半分なので、\(\displaystyle\frac{(n-1)!}{2}\) となる。
それぞれ、問題文を見て使い分けを見極めましょう。
さいごまで記事を読んでいただきありがとうございました！
「30分で集中力が切れてしまう方へ」
勉強の集中力UPのために
子供に集中して宿題をさせるために
会議やプレゼンのタイムマネジメントのために
ポチップ
質問や感想はコメントへ！