【場合の数】『塗り分け』特定の場所に着目することによりパターンを絞っていく

塗り分けの場合の数

今回は塗り分けの問題です。

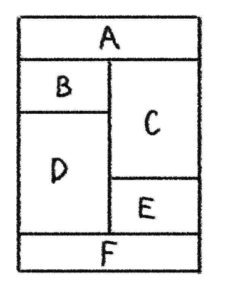
上図を色で塗り分ける方法は何通りあるのか？という問題です。こういった問題では、大抵同じ色で塗られた領域は隣接しない場合がほとんどです。例えば、$A$ と $B$ の両方に赤が塗られるようなことはないわけです。ただし、同じ色どうしが隣り合わなければいいので、以下のような場合は大丈夫です。

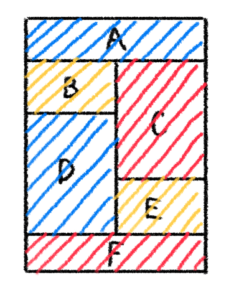
このような問題は、定期テストや模試などで頻出となっています。塗り分けの問題を考えるにあたってのポイントがいくつかあるので、それを押さえていきましょう！

今回の図だと、$C$ または $D$ がより多くの領域と接していますね！

場合の数のパターンを見つけるコツ

場合の数を解く上で重要になるのが、何かしらの規則性、つまりパターンを見つけられるかどうかですよね。しかし、いくら眺めていても全くパターンが見つけられないという経験をしたことがある方は多いのではないでしょうか？そういうとき、どうすれば良いのでしょう？それは、試しに何かを入れてみることです。つまり、具体例を自分で考えてみるのです。具体例を考えてみることは、今回の問題に限らず、数学の問題を解く際にとても役立つので、ぜひ覚えておきましょう。色分けが赤、青、黄、緑の $4$ 色で行われる問題であれば、まずは特別な領域の一つである $C$ に赤を入れてみます。もちろん、 $D$ に入れてみても構いません。そうすると、$A$ には赤以外の色なので、試しに青を入れてみて、$B$ には赤と青以外の色なので、黄色を入れてみます。すると、以下のような色分けとなりますね。

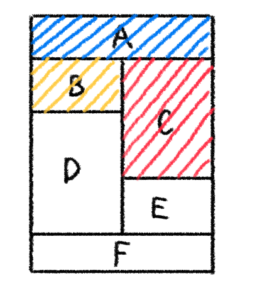
ということは、 $D$ には青か緑の $2$ 択、 $E$ には $C$ と $D$ 以外の色なので $2$ 択、のように少しずつ思考が進みますね。分かりにくい問題であっても、何もできずにギブアップするより、このように少しでも思考を進めることができる方が、まだ解ける希望を感じることができますね。「試しにいろいろ入れてみる。」ぜひ行き詰った時に使ってみましょう！

塗り分け（問題）

ある領域が、図のように $6$ つの区画に分けられている。境界を接している区画は異なる色で塗るとして、赤・青・黄・緑の $4$ 色以内で領域を塗り分ける方法は何通りあるか。

塗り分け（答案の例）

$3$ 色で構成される場合と、 $4$ 色で構成される場合を考える。まず、$C$,　$A$,　$B$ に色が隣り合わないように入れていく方法は、${}_4{P}_3=4\times 3\times 2=24$ 通りだけある。

次に $D$ に入る色は、$B$ と $C$ に入っている色以外なので、 $2$ 通り。

$E$ に入る色は、$C$ と $D$ に入っている色以外なので、 $2$ 通り。

$F$ に入る色は、$D$ と $E$ に入っている色以外なので、 $2$ 通り。

よって、${}_4{P}_3\times 2\times 2\times 2=192$

塗り分け（解説）

今回は $4$ 色以内で塗り分ける方法を考える問題ですが、お分かりの通り、$1$ 色や $2$ 色だけで塗り分けることはできません。よって、$3$ 色で塗り分ける場合と $4$ 色で塗り分ける場合の合計を求める問題となります。まず、特別な領域 $C$ から考えていきましょう。
※　特別な領域とは、この記事の最初の方に書いたように、多くの領域と隣り合ってる領域のことです。今回の問題では、 $C$ や $D$ がそれにあたります。

$C$ は何色でもいいので、$4$ 色の中から $1$ 色を選びます。
⇨ $4$ パターン
※　考えやすいように具体的に色を当てながら進めていきます。試しに、赤を入れたと仮定します。

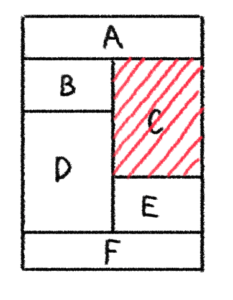
残りの領域は、順番に考えていきます。
$A$ には、$C$ に入れた色以外の $3$ 色の中から $1$ 色を選びます。
⇨ $3$ パターン
※　今回は、青を入れたとします。

$B$ には、$C$ と $A$ に入れた色以外の $2$ 色の中から $1$ 色を選んで入れます。
⇨ $2$ パターン
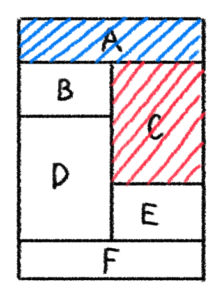
※　今回は、黄を入れたとします。

ここからは、$D$,　$E$,　$F$ に入る色によって、$3$ 色で構成されるのか $4$ 色で構成されるのかが決まります。

例えば、

$D$,　$E$,　$F$ それぞれに青、黄、赤を入れると、$3$ 色で構成されます。
$D$,　$E$,　$F$ それぞれに、例えば緑、青、赤を入れると、$4$ 色で構成されます。

しかしここで大事なのは、これらは同時に考えることができる、ということです。つまり、場合分けが必要ないのです。具体的に解説を進めていきましょう。

$D$ には、$B$ と $C$ に入れた色以外の $2$ 色の中から $1$ 色を選んで入れます。
⇨ $2$ パターン
※　今回は、緑を入れたとします。

$E$ には、$C$ と $D$ に入れた色以外の $2$ 色の中から $1$ 色を選んで入れます。
⇨ $2$ パターン
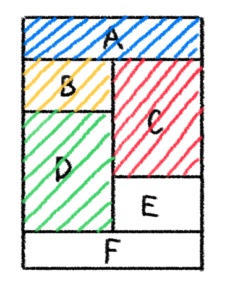
※　今回は、青を入れたとします。

$F$ には、$D$ と $E$ に入れた色以外の $2$ 色の中から１つ選んで入れます。
⇨ $2$ パターン
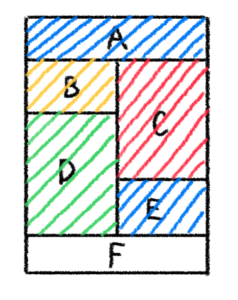
※　今回は、赤を入れたとします。

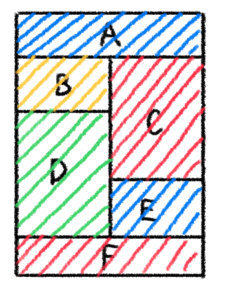
よって、$4\times 3\times 2\times 2\times 2\times 2=192$ となります。

これが $4$ 色で塗り分けるパターンの合計です。しかし、今回はあえて $4$ 色すべてを使うような具体例を考えましたが、この考え方には、以下のような場合も含まれていますね。

つまり、$3$ 色だけで構成されるパターンも、この思考には含まれているわけです。よって、$3$ 色で構成されるパターンと $4$ 色で構成されるパターンを同時に求めたことになり、今回の答えは $192$ 通りとなるわけです。

4色すべてを使って塗り分けるとき

今回の解説は上記の内容で終了ですが、$4$ 色すべてを使って塗り分けるという条件の問題もあるので、そちらの解き方も載せておきますね。

（$4$ 色すべてを使って塗り分ける）
=（$4$ 色までで塗り分ける）$-$（$3$ 色だけで塗り分ける）
となります。

今回の記事で取り上げた問題で、「$4$ 色までで塗り分ける」場合は計算しました。よって、あとは「$3$ 色だけで塗り分ける」場合を計算すれば、$4$ 色すべてを使って塗り分ける方法を計算することができるということになります。

＜$3$ 色だけで塗り分ける方法＞

そもそも、使用する $3$ 色を、 $4$ つの色の中から選ぶ必要があります。

よって、${}_4{C}_3={\displaystyle \frac{{}_4{P}_3}{3!}={\displaystyle \frac{4\times 3\times 2}{3\times 2\times 1}=4}}$

※　今回は、赤・青・黄を使用するとして考えます。

まず、特別な領域 $C$ から入れていきます。

$C$ には、$3$ 色の中から１つ選んで入れます。
⇨ $3$ パターン
※　今回は、赤を入れたとします。

残りは先程の問題同様、順番に考えていきます。

次に、$A$ には、$C$ に入れた色以外の$2$ 色の中から１つ選んで入れます。
⇨ $2$ パターン
※　今回は、青を入れたとします。

次に、$B$ には、$A$ と $C$ に入れた色以外の色を入れます。
⇨ $1$ パターン
※　今回は、赤と青はすでに使用しているので、黄色を入れるしかありません。

次に、$D$ には、$B$ と $C$ に入れた色以外の色を入れます。
⇨ $1$ パターン
※　今回は、赤と黄はすでに使用しているので、青を入れるしかありません。

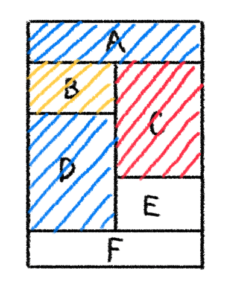
次に、$E$ には、$C$ と $D$ に入れた色以外の色を入れます。
⇨ $1$ パターン
※　今回は、赤と青はすでに使用しているので、黄を入れるしかありません。

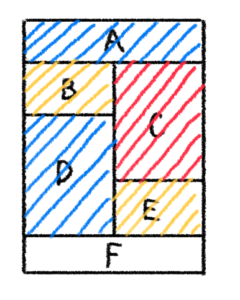
次に、$F$ には、$D$ と $E$ に入れた色以外の色を入れます。
⇨ $1$ パターン
※　今回は、青と黄はすでに使用しているので、赤を入れるしかありません。

よって、$3$ 色で塗り分ける場合は

$3\times 2\times 1\times 1\times 1\times 1=6$
${}_4{C}_3\times 6=24$

通りということになります。

これにより、

（$4$ 色すべてを使って塗り分ける）
=（$4$ 色以内で塗り分ける）$-$（$3$ 色だけで塗り分ける）
=$192-24$
=$168$ 通りとなるわけです。

おわりに

今回は、塗り分けの問題でした。

解説の途中に書かれている、「特別な領域から考える」が大きなポイントでした。

特別な領域から考える考え方がよくわからない方はご連絡ください。また、オンラインで家庭教師も可能です。