区分求積法
今回は区分求積法について解説していきます!
区分求積法は、なめらかな関数に囲まれた部分の面積を求めるための方法です。
例えば、以下のような図形であれば赤い部分と青い部分で分けて計算することができますね。
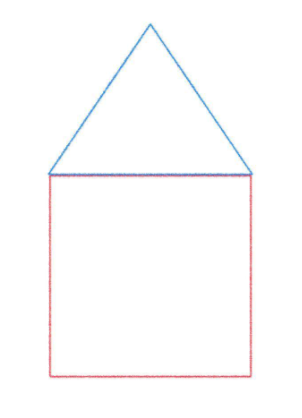
このように求めたい面積を複数個に分けて計算する方法を、なめらかな曲線に応用させようと昔の数学者は考えました。
以下のように、細かく長方形に分割して足していくというものです。
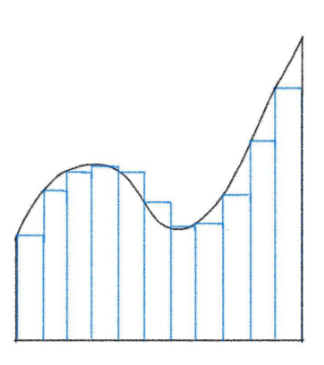
では、実際にどういう式で計算していくかを解説していきます!
区分求積法(説明)
関数 \(f(x)\) が閉区間 \([a\), \(b]\) で連続であるとき、この区間を \(n\) 等分して両端と分点を順に \(a=x_0\), \(x_1\), \(x_2\), \(\cdots\) , \(x_n=b\) とすると、
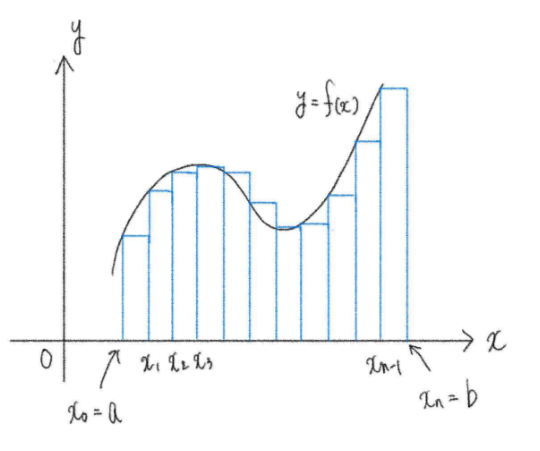
また、\(\displaystyle\frac{b-a}{n}=\Delta x\) とおくと、
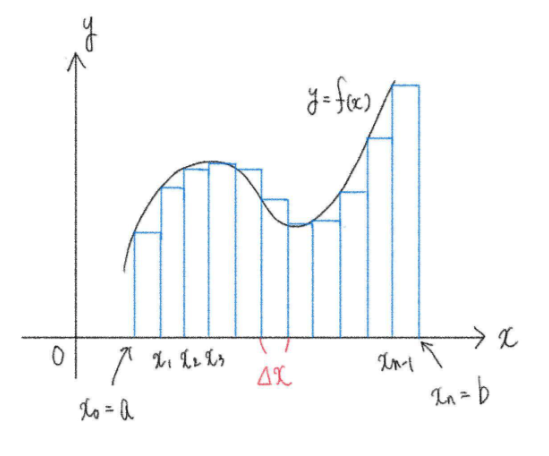
\(\displaystyle\int_{a}^{b} f(x) dx=\lim_{n\to\infty}\sum_{k=1}^n f(x_k)\Delta x\)
〈式の解説〉
① \(\Delta x=\) 横、\(f(x_k)=\) 縦と見立てると、\(f(x_k)\cdot x_k\) は青い長方形の面積となる。
② \(n\) 個の青い長方形を足し合わせるので、\(\displaystyle\sum_{k=1}^n\) \(f(x_k)\Delta x\) となる。
③ 青い長方形を細かくすればするほど(\(n\) を無限に近づけるほど)正しい面積の値に近づくので、\(\displaystyle\lim_{n\to\infty}\) \(\displaystyle\sum_{k=1}^n f(x_k)\Delta x\)
特に、\(a=0\), \(b=1\) のとき、\(\Delta x=\displaystyle\frac{1}{n}\), \(x_k=\displaystyle\frac{k}{n}\) で
\(\displaystyle\int_{1}^{0} f(x)dx=\lim_{n\to\infty}\displaystyle\frac{1}{n}\sum_{k=1}^nf\big(\frac{k}{n}\big)\)
区分求積法(問題)
\(\displaystyle\lim_{n\to \infty}\sum_{k=1}^n \big(\frac{n+k}{n^4}\big)^{\frac{1}{3}}\) の極限値を求めよ。
>>詳細はこちらから
(解説)
\(\displaystyle\int_{1}^{0} f(x)dx=\lim_{n\to\infty}\displaystyle\frac{1}{n}\sum_{k=1}^nf\big(\frac{k}{n}\big)\) \(\cdots\) ※
\(\big(\displaystyle\frac{n+k}{n^4}\big)^{\frac{1}{3}}=\big(\displaystyle\frac{n+k}{n^3\cdot n}\big)^{\frac{1}{3}}\)
\(=\displaystyle\frac{1}{n}\big(\frac{n+k}{n}\big)^{\frac{1}{3}}\)
\(=\displaystyle\frac{1}{n}\big(1+\frac{k}{n}\big)^{\frac{1}{3}}\)
よって
\(S=\displaystyle\lim_{n\to\infty}\displaystyle\frac{1}{n}\sum_{k=1}^n \big(1+\frac{k}{n}\big)^{\frac{1}{3}}\)
ここで、※の公式に当てはめると、
\(=\displaystyle\int_0^1 (1+x)^{\frac{1}{3}} dx\)
\(=\big[\displaystyle\frac{3}{4}(1+x)^{\frac{4}{3}}\big]_0^1\)
\(=\displaystyle\frac{3\sqrt[3]{2}}{2}-\frac{3}{4}\)
おわりに
さいごまで読んでいただきありがとうございました!
- 大学受験数学で困っている方
- 公務員試験の数学で困っている方
- 統計学(統計検定)の勉強で困っている方
個人家庭教師やってるので、ぜひコメントやXでご連絡ください。(Xはこちら)
私自身、数学に関して順風満帆に理解できてきたわけではありませんでした。
周りを見渡せば数学の天才がゴロゴロいて、そんな人たちに比べれば私は足元にも及びませんでした。
だからこそ、わからない、理解できない方の気持ちを少しはわかってあげられると自負しております。
数学に困っている方の一助になれれば幸いです。
ご連絡お待ちしております。





質問や感想はコメントへ!