回転体の体積
切り口の面積の関数 \(S(x)\) が与えられている時、
\(x=a\) から \(x=b\) までの体積を \(V\) とする。また、ある \(x\) 座標で切り取った立体の切り口の面積を \(S(x)\) とすると、
$$V=\displaystyle\int_b^a S(x)dx$$
※ イメージ:\(S(x)\) を \(x=a\) から \(x=b\) まで足し合わせていくイメージ
切り口の面積の関数 \(S(x)\) が与えられておらず、代わりに曲線 \(f(x)\) が与えられている時、
切り口の面積の関数 \(S(x)\) は与えられていないことの方が多く、その代わりに曲線 \(f(x)\) が与えられている。
その場合、曲線 \(y=f(x)\) と \(x\) 軸と \(2\) 直線 \(x=a\), \(x=b\) で囲まれた部分を \(x\) 軸の周りに \(1\) 回転してできる回転体の体積 \(V\) は、
$$V=\pi\displaystyle\int_a^b \{f(x)\}^2 dx=\pi\int_a^b y^2 dx$$
\(2\) つの曲線 \(y=f(x)\), \(y=g(x)\) が与えられている時、
\(2\) つの曲線 \(y=f(x)\), \(y=g(x)\) と \(2\) 直線 \(x=a\), \(x=b\) で囲まれた部分を \(x\) 軸の周りに \(1\) 回転してできる回転体の体積 \(V\) は、
$$V=\pi\displaystyle\int_a^b |\{f(x)\}^2-\{g(x)\}^2| dx$$
回転体の体積(問題)
次の曲線や座標軸で囲まれた部分を \(x\) 軸の周りに \(1\) 回転させてできる立体の体積 \(V\) を求めよ。
(1) \(y=1-\sqrt{x}\), \(x\) 軸, \(y\) 軸
(2) \(y=1+\cos x\) (\(-\pi\leq x\leq \pi\)), \(x\) 軸
>>詳細はこちらから
回転体の体積(解説)
(1) \(1-\sqrt{x}=0\) とすると、\(\sqrt{x}=1\) よって \(x=1\)
ゆえに、
\begin{eqnarray} V &=& \pi\int_0^1 (1-\sqrt{x})^2 dx\\ &=& \pi\int_0^1 (1-2\sqrt{x}+x) dx\\ &=& \pi\big[x-\displaystyle\frac{4}{3}x\sqrt{x}+\frac{1}{2}x^2\big]_0^1\\ &=& \pi\big(1-\displaystyle\frac{4}{3}+\frac{1}{2}\big)\\ &=& \displaystyle\frac{\pi}{6} \end{eqnarray}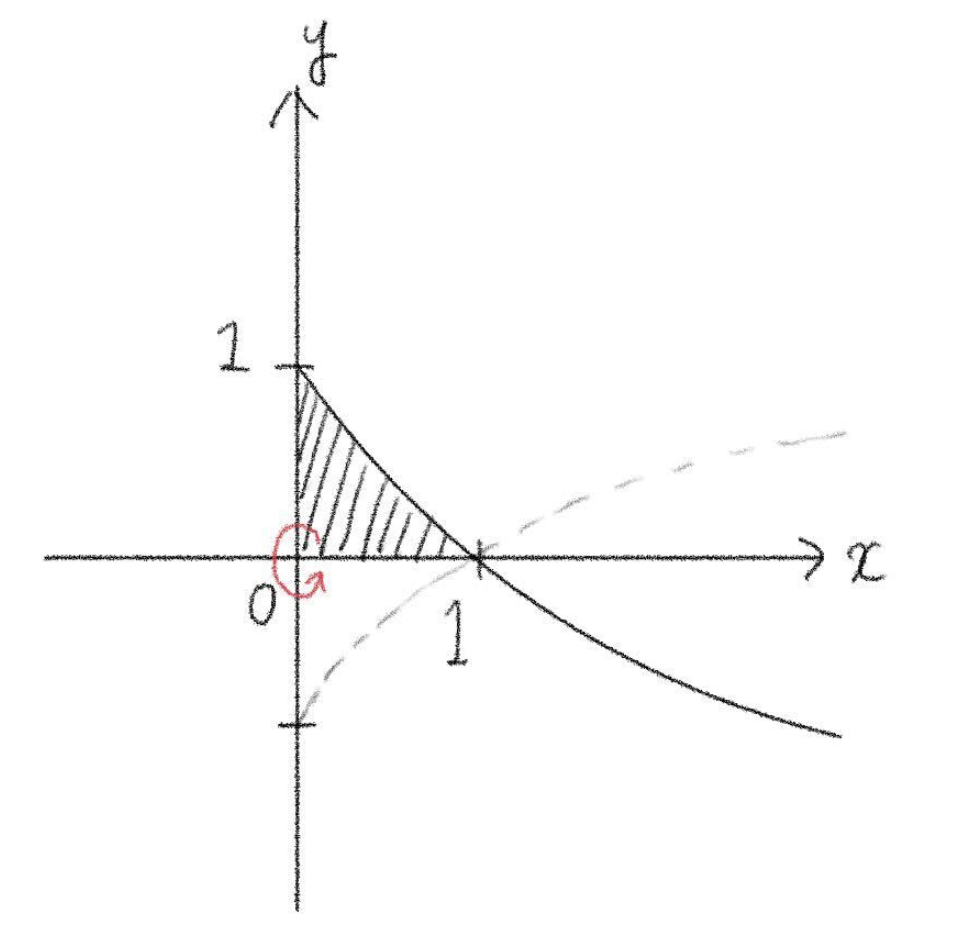
(2) \(1+\cos x=0\) とすると、\(-\pi\leq x\leq\pi\) では \(x=\pm\pi\)
\begin{eqnarray} V &=& \pi\int_{-\pi}^{\pi} (1+\cos x)^2 dx\\ &=& 2\pi\int_0^{2\pi} (1+\cos x)^2 dx\\ &=& 2\pi\int_0^{2\pi} (1+2\cos x+\cos^2 x)dx\\ &=& 2\pi\int_0^{2\pi} \big(1+2\cos x+\displaystyle\frac{1+\cos 2x}{2}\big) dx\\ &=& 2\pi\int_0^{2\pi} \big(\displaystyle\frac{3}{2}+2\cos x+\frac{1}{2}\cos 2x\big) dx\\ &=& 2\pi\big[\displaystyle\frac{3}{2} x+2\sin x+\frac{1}{4}\sin 2x\big]_0^{\pi}\\ &=& 2\pi\cdot\displaystyle\frac{3}{2}\pi=3\pi^2 \end{eqnarray}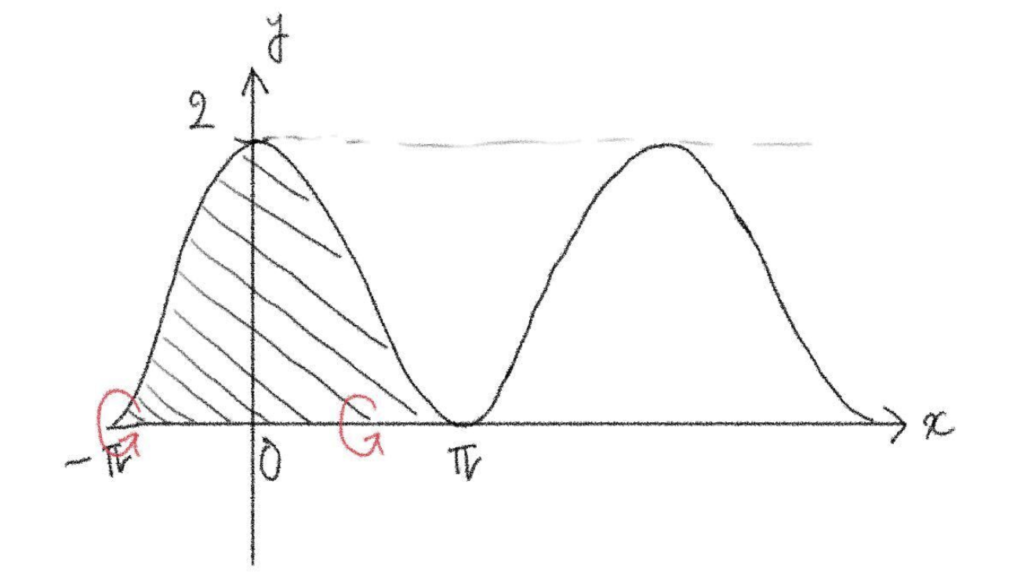
おわりに
さいごまで読んでいただきありがとうございました!
【最新】こちらの記事がおすすめ!





