今回はグラフの最大と最小を求める問題です。
例えば上記のグラフであれば、
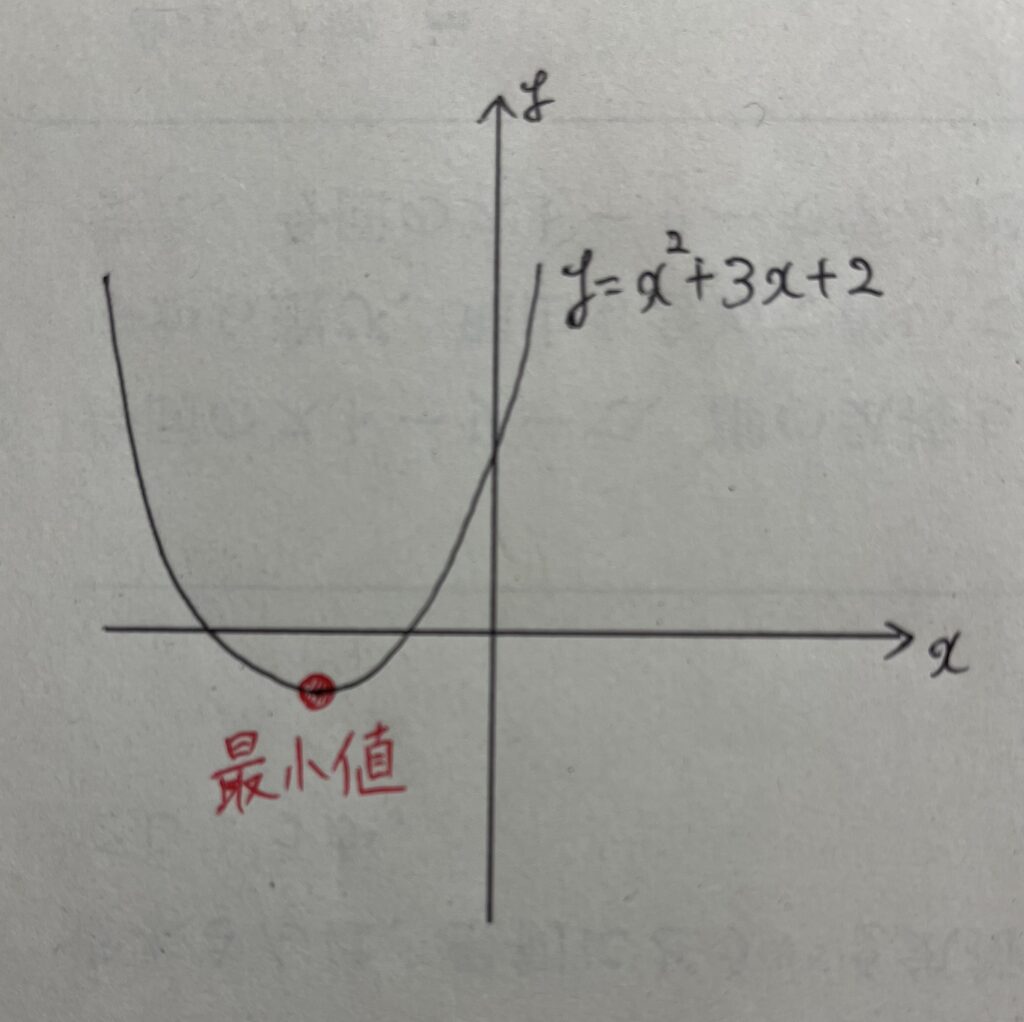
変域によって範囲が区切られていれば、その中での最大と最小がわかるため、「最大値と最小値を求めなさい。」と言われたら、以下の
・
・グラフの変域
例えば、
これを頭に置きながら、以下の問題を見ていきましょう。
最大値と最小値(問題)
実数
>>詳細はこちらから
最大値と最小値(答案の例)
また、
ここで、
により、グラフの頂点は(
また、
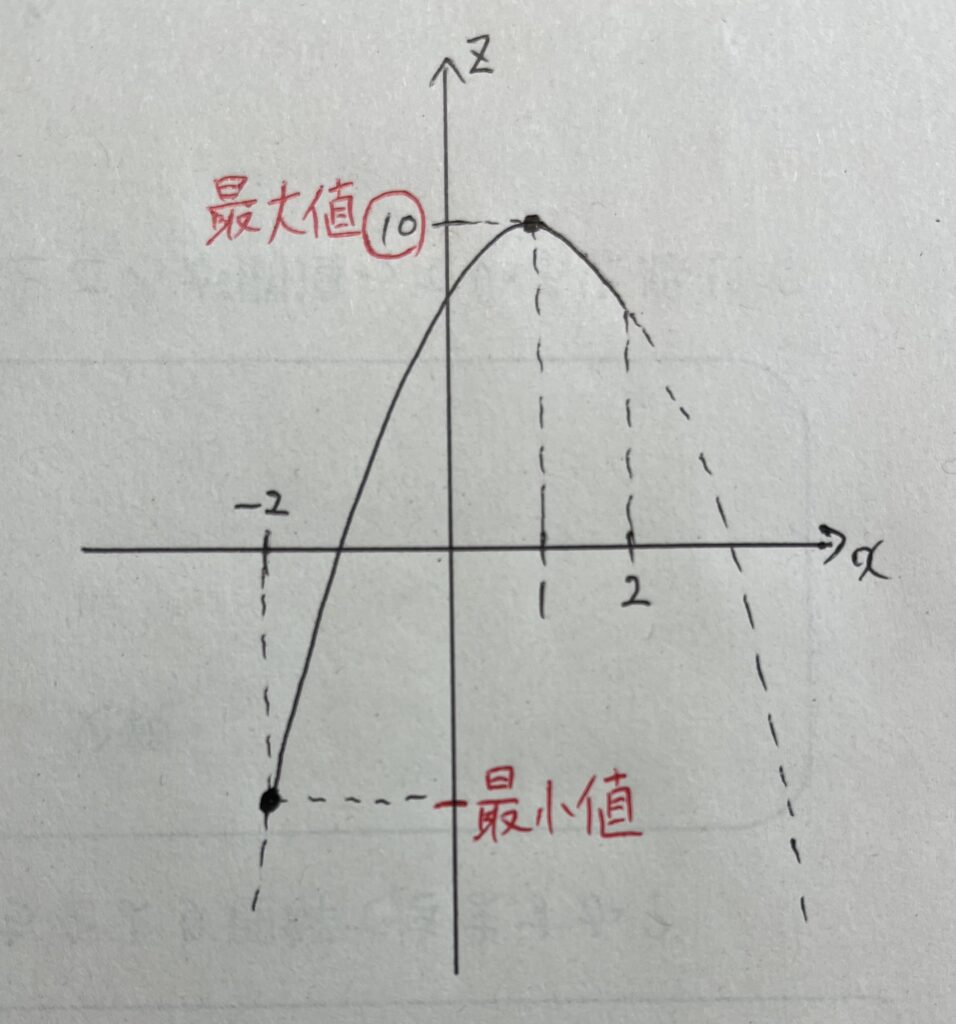
最小値は、
また、最小値をとるときの
つまり、
したがって、
をとる。
最大値と最小値(解説)
まず、多くのことが複雑に起こっているので、状況を整理しましょう。
冒頭で、最大・最小を求める際に必要なものは
まずはそれらを作っていきましょう。
ひとまず、変域から探っていきます。
変域は、必ず不等式の形になっていますね。
しかし、現在問題文には不等式がありません。
ないのであれば、作ればいいのです。
でも、どうやって??
こういう場合、疑うべきは
<正の数を
<負の数を
<
よって、問題で登場している
しかし今、問題では「
「片方ずつについては
簡単です。
「
今回は、
とします。ここで左辺を見れば、
という不等式を導けるわけです。このようにして、不等号を生み出すのです。そして、
とも言えるわけですね。これを変形し、
という変域を作ることができます。次に、肝心のグラフを作っていきます。
などのように、
① 等式になっている(イコールが含まれている)
② 等式の右辺は、文字が
という特徴をもっています。まず、①について考えていきます。グラフの式がなぜ等式になっているかというと、
ここで、
のように、
この
としたかったのです。そこで、
のようにしました。そうすることで、
(みなさんは式と言えば
例えば、
(縦軸が
文字はあくまでもそこにある数を代入しますよ、ということを表すものなので、ちなみに横軸に使われている
さて、話を元に戻しましょう。
イコールになっていない状態の
となります。しかしこれでは、文字が
という式が出てきていますね。これを使って
となりますね。よって、このグラフを書いて、上記で求めた
により、頂点は(
つまり、
ということになります。しかし、
となるわけですね。
この手の問題は、条件式をどう使うかが鍵です。
ぜひたくさんのパターンに触れながら、傾向を掴んでいきましょう。
おわりに
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。



