これから公務員試験数学範囲の勉強を始める方へ
まずは、『範囲と対策方法』を知りましょう!
数量関係(りんごとなしとオレンジ)
今回は数量関係についての問題を扱っていきます!
数量関係とは、事象の中の数量や、増加や合併などの場面、数の大小などの関係に目を付けること
今回扱う問題は、
曖昧な表現の中から”確実に言えること” を探していきます。
まずは実際に扱う問題を見ていきましょう。
ある店で、りんご 円、なし 円、オレンジ 円で販売している。 と の購入について次のことがわかっているとき、確実にいえるのはどれか。
・ は 円分、 は 円分買った。
・ と の買ったなしの個数の差は 個であった。
・ の購入個数はオレンジよりりんごの方が多かった。
見ての通り、りんごとなし、オレンジの具体的な値段は書かれているものの、何個購入したかまでは明記されていません。
購入数はわかりませんが、「 は 円分、 は 円分買った。」と合計金額はわかってたり、「 と の買ったなしの個数の差は 個」のような曖昧な情報がいくつか並んでいます。これらの情報から確実に言えることを選択肢から選ぶ問題となっています。
変数を文字に置いて解く方法もありますが、そうではなく、「○○なら△△」「△△なら□□」のように演繹的に導いていく方法もあります。公務員試験の問題ではそこまで複雑な問題は出題されないため後者の方法で解いていくのが良いかもしれません。
では、解法を見ていきましょう。
数量関係(問題)
ある店で、りんご 円、なし 円、オレンジ 円で販売している。 と の購入について次のことがわかっているとき、確実にいえるのはどれか。
・ は 円分、 は 円分買った。
・ と の買ったなしの個数の差は 個であった。
・ の購入個数はオレンジよりりんごの方が多かった。
1. はりんごを 個買った。
2. は全部で 個買った。
3. はオレンジとりんごのみを買った。
4. はオレンジを最も多く買った。
5. と でオレンジを 個買った。
解説
つ目の条件より、
の合計で十の位の 円より、 円を作ることができる「なし」を何個買ったかを考える。十の位を にするには、なしで を作って、りんごの を足し算することで十の位を にする。
このことより、 は「なし」を 個、 個、 個、 個 となるが、 個以上買うと「なし」だけで 円を超えてしまうので、なしの個数は 個か 個となる。
同様に の十の位が なので、 は「なし」を 個、 個、 個 となるが、 個以上買うと「なし」だけで 円を超えてしまうので、なしの個数は 個か 個となる。
つ目の条件より、
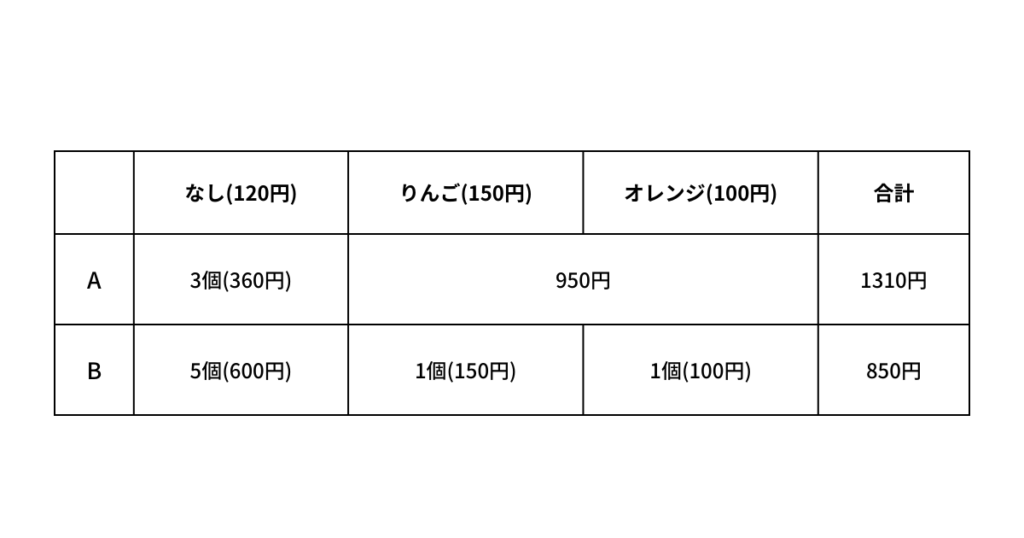
「なし」の個数の差が 個なので、 が 個、 が 個と確定する。 は残り 円分となるので、りんご 個、オレンジ 個と決まる。

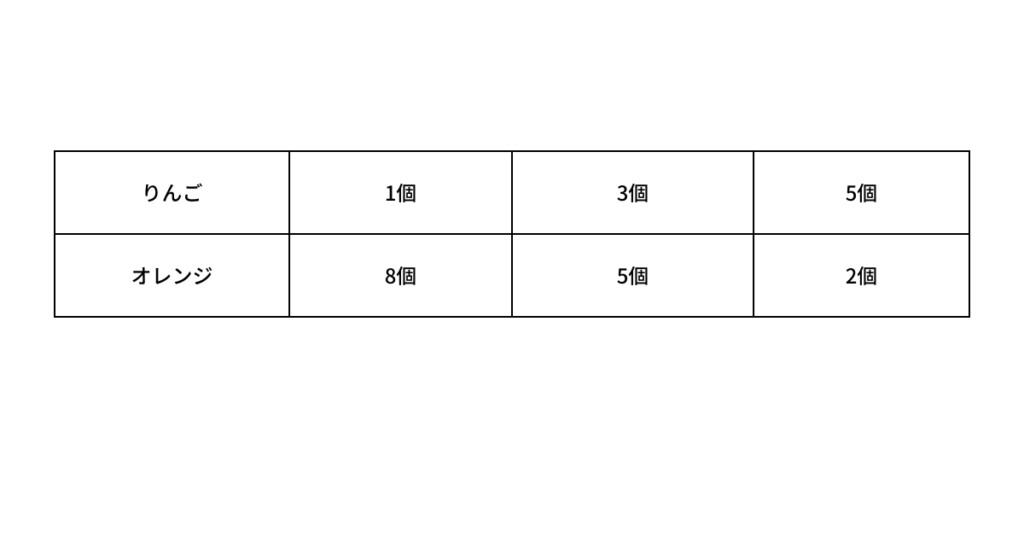
は残りは 円となる。この 円を作るにはりんごを奇数個買ったことになる。りんごとオレンジの個数の可能性は以下のようになる。

しかし、 つ目の条件より、
りんごのほうを多く買っているので、りんごが 個、オレンジが 個と確定する。
以上より、正答は である。
おわりに
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。