【データサイエンス】『重回帰分析』母親の学力と年齢が子供の学力にどれだけ影響を与えるのか？

子供の学力は母親に依存する？

今回は、Kaggleに公開されているデータセットを用いて子供の学力が母親によってどれだけ決められるのかを解析してみようと思います。

「母親によって」とは、今回は”母親の学歴”と”子供を出産した時の年齢”とします。また、”母親の学歴”は \(1=\) 高校未学歴、\(2=\) 高校卒業、\(3=\) 大学中退、\(4=\) 大学卒業とダミー変数を用いて表します。

解析手法選定

今回は、重回帰分析を用います。

特徴量が”子供を出産した時の年齢”と”母親の学歴”のみのため、この2種で子供の学力を表してしまうのはいささか論理が飛躍していると言わざるを得ない。しかし、どちらの特徴量がより子供の学力に影響を及ぼすのかという比較にはなる。また、今後特徴量が増えた際の研究拡大につながると考え解析に至った。

重回帰分析

データセットの読み込みと中身

まずは、データセットを読み込ませます。

import pandas as pd

# CSVファイルのパスを指定
file_path = 'child_iq.csv'

# CSVファイルを読み込む
df = pd.read_csv(file_path)

# データフレームの内容を表示
print(df)

〈出力結果〉

Unnamed: 0  ppvt  educ_cat  momage
0             1   120         2      21
1             2    89         1      17
2             3    78         2      19
3             4    42         1      20
4             5   115         4      26
..          …   …       …     …
395         396    87         3      21
396         397    69         2      20
397         398    80         1      25
398         399    98         1      18
399         400    81         2      22

※データセットはKaggleから無料でDLできます。

説明変数と目的変数へ分解

#目的変数と説明変数への分解
Y = df['ppvt']
X = df[['educ_cat', 'momage']]
print(Y)
print(X)

〈出力結果〉
上が目的変数、下が説明変数

0      120
1       89
2       78
3       42
4      115
      … 
395     87
396     69
397     80
398     98
399     81

   educ_cat  momage
0           2      21
1           1      17
2           2      19
3           1      20
4           4      26
..        …     …
395         3      21
396         2      20
397         1      25
398         1      18
399         2      22

重回帰分析モデルの作成

#重回帰分析モデルの作成
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)

model = LinearRegression()
model.fit(X_train, Y_train)

テストデータに対する予測

# テストデータに対する予測
Y_pred = model.predict(X_test)

〈出力結果〉

モデルの評価

#【モデルの評価①_決定係数と平均二乗誤差】
mse = mean_squared_error(Y_test, Y_pred)
r2 = r2_score(Y_test, Y_pred)

〈出力結果〉

Mean Squared Error: 367.49876637463524
R-squared: -0.01695673154442834

決定係数と平均二乗誤差の数字だけで、
回帰係数が目的変数を全く説明できていないことは明らかだが、念の為可視化させておく。

#【モデルの評価②_予測結果の可視化】
plt.scatter(Y_test, Y_pred, color='blue', edgecolors='k')
plt.plot([min(Y_test), max(Y_test)], [min(Y_test), max(Y_test)], color='red', lw=2)
plt.xlabel('実際の値')
plt.ylabel('予測値')
plt.title('実際の値 vs 予測値')
plt.show()

〈出力結果〉

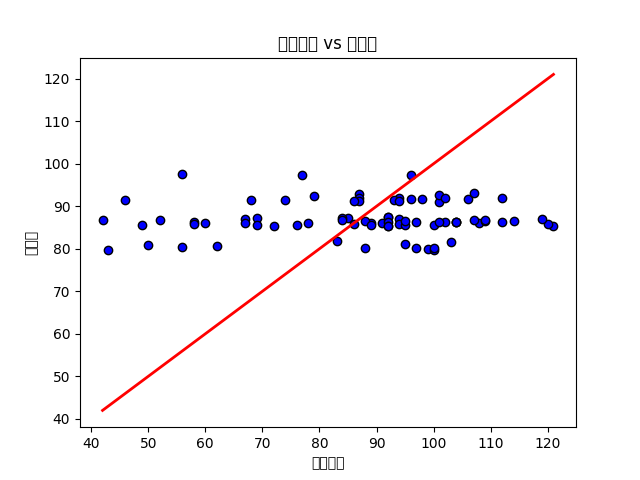
\(x\) 軸が”実際の値”、\(y\) 軸が “予測値”を表している。実際に値と予測値が近ければ近いほど、モデルは上手くできていると言え、赤線 \(y=x\)の上にプロットされる。見てわかるように実際の値と予測値に大きく乖離があり、決定係数は \(0\) に近くなり、平均二乗誤差は大きくなってしまうことがわかる。

今回の解析に対する解釈とネクストアクション

求められた回帰係数から以下の式が与えられる。

$$Y=5.484\times (親の学力)+0.221\times (子供が生まれた親の年齢)+70.215$$

となり、一見すると”子供が産まれた年齢”よりも”親の学力”がより影響を与えてる気もしなくもない。しかし、今回のデータを眺めると、子供が産まれた年齢が

$$(min,max)=(17,29)$$

となり、データ数に比べて範囲が狭い。また、”親の学力”が \(1\)〜\(4\) とダミー変数を用いてることから目的変数を上手く説明できなかったと考えられる。

ネクストアクションは、”子供が産まれた親の年齢”の範囲をより広げ、”親の学力”をダミー変数ではなく、数値で表すことで目的変数をより表すことができると考えられる。

おわりに

さいごまで記事を読んでいただきありがとうございました！

「30分で集中力が切れてしまう方へ」

 勉強の集中力UPのために

 子供に集中して宿題をさせるために

 会議やプレゼンのタイムマネジメントのために

【ランキング1位受賞♪】【正規販売店】タイムタイマー モッド ホームエディション Time Timer 知育時計 タイマー 子ども 子供 キッズ 正規品 知育 学習 時間 時刻 コンパクト 勉強 リビング学習 カウントダウン 静か おしゃれ アナログ シンプル ストップウォッチ TTM9

掛け時計 専門店 allclocks

¥3,960 （2024/09/05 22:40時点 | 楽天市場調べ）

Amazon

楽天市場

Yahooショッピング

メルカリ

ポチップ