【統計学の基礎】正規分布

URLをコピーしました！

正規分布とは
1. 正規分布の基本的な性質
2. 正規分布の応用
中心極限定理
正規分布の限界
例題
1. 例題1: 学生のテストスコアの分析
2. 例題2: 製品の重量管理
まとめ

正規分布とは

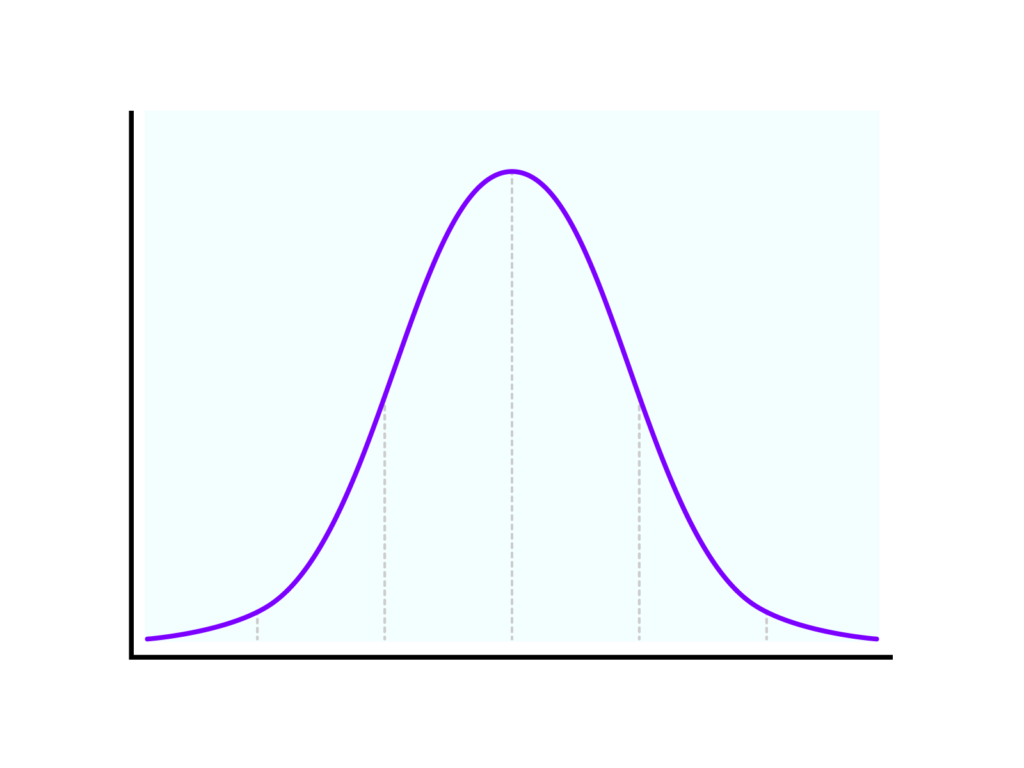
正規分布は、データの分布を表す基本的な方法の一つです。形が釣鐘（つりがね）型をしているので、「ベルカーブ」とも呼ばれます。この分布は、自然現象や社会現象の多くに見られる特徴的なパターンを示します。

$f (x) = \frac{1}{\sqrt{2 π σ^{2}}} e^{(- \frac{(x - μ)^{2}}{2 σ^{2}})}$

$x$ ：データの値
$μ$ ：平均
$σ$ ：標準偏差

この数式は、特定の値が現れる確率を計算します。また、平均が $0$ 、標準偏差が $1$ の特別な正規分布を標準正規分布と言います。この分布を使うと、さまざまな正規分布を簡単に比較することができます。

正規分布の基本的な性質

釣鐘型の形状：正規分布は平均値を中心として左右対称の形をしています。これにより、データの多くが平均値の周りに集中し、遠く離れるほどデータの数が減ることがわかります。

平均と標準偏差：正規分布は平均（ $μ$ ）と標準偏差（ $σ$ ）という2つの値で決まります。平均はデータの中心、標準偏差はデータのばらつきを示します。

68-95-99.7ルール：正規分布では、データの約 $68$ %が平均 $\pm 1$ 標準偏差の範囲内に、約 $95$ %が平均 $\pm 2$ 標準偏差の範囲内に、約 $99.7$ %が平均 $\pm 3$ 標準偏差の範囲内に収まります。

正規分布の応用

正規分布は多くの分野で使われています。以下にいくつかの例を挙げます。

自然科学：身長や体重、血圧など、多くの身体的特徴が正規分布に従います。

社会科学：収入や消費のデータも正規分布に近いことが多く、経済分析に使われます。

品質管理：製品の寸法や性能のばらつきを評価するのに使われます。これにより、品質を保ち、不良品を減らすことができます。

教育：テストの点数や成績の評価にも使われます。これにより、学生のパフォーマンスを公平に比較できます。

中心極限定理

中心極限定理は、大量の独立した同じ分布に従うデータを集め、その平均を求めると、その平均値は元の分布がどんな形であっても、最終的には正規分布に近づくというものです。

具体的には、母集団の分布が歪んでいたり、ばらつきが大きかったりしても、十分なサンプルサイズがあれば、サンプル平均の分布は正規分布に収束します。これにより、データの母集団の分布がわからなくても、統計的推測がしやすくなります。

〈中心極限定理のポイント〉

サンプルサイズの重要性：サンプルサイズが大きくなるほど、サンプル平均の分布は正規分布に近づきます。一般に、サンプルサイズが $30$ を超えると、ほとんどの場合で正規分布に近くなります。

母集団分布の不問：元のデータがどのような分布をしていても、この理論が成り立ちます。例えば、偏った分布や多峰性の分布であっても、サンプル平均の分布は正規分布に近づきます。

実用性：中心極限定理により、多くの統計的手法が正規分布を仮定して成り立っていることが説明されます。これにより、実際のデータ分析で頻繁に用いられます。

正規分布の限界

正規分布は非常に便利ですが、すべてのデータに適用できるわけではありません。

偏ったデータ：データが左右対称でない場合、正規分布は適しません。

極端な値が多いデータ：金融市場の価格変動のように、極端な値が多い場合は、他の分布を使うことが適しています。

正規分布は、自然現象や社会現象においてデータの分布を記述するために広く利用される統計モデルです。多くの実世界のデータが正規分布に従うことから、統計分析や機械学習などで頻繁に用いられます。ここでは、正規分布を活用した簡単な例題を2つ挙げて、その解説を行います。

例題

例題1: 学生のテストスコアの分析

あるクラスの学生 $30$ 人が数学のテストを受け、その点数は平均 $75$ 点、標準偏差 $10$ 点の正規分布に従っていると仮定します。このテストのスコアが $70$ 点以下の学生の割合を求めてください。

（解説）

平均と標準偏差の設定
テストの平均が $75$ 点、標準偏差が $10$ 点です。
標準偏差はデータのばらつきを表し、テストスコアの分布がどれくらい広がっているかを示します。

確率計算
正規分布の累積分布関数を使って、特定の点数以下の割合を計算できます。
累積分布関数は、ある点数までのデータの合計確率を求める関数です。ここでは、 $70$ 点以下の割合を計算します。

標準化
正規分布を標準正規分布（平均 $0$ 、標準偏差 $1$ ）に変換します。計算式は次の通りです。

$Z = \frac{X - μ}{σ}$

ここで、 $X$ は特定の点数、 $μ$ は平均、 $σ$ は標準偏差です。
この場合、 $X = 70$ 、 $μ = 75$ 、 $σ = 10$ なので、

$Z = \frac{70 - 75}{10} = - 0.5$

累積分布関数を使用
標準正規分布の表または計算ツールを使って、 $Z = - 0.5$ のときの値を見つけます。標準正規分布表によると、 $Z = - 0.5$ に対応する値は約 $0.3085$ です。

結果の解釈
したがって、このクラスの学生の約 $30.85$ %が、 $70$ 点以下のスコアを取っていることが分かります。

例題2: 製品の重量管理

ある工場で生産される部品の重量は、平均 $500$ g、標準偏差 $20$ gの正規分布に従っているとします。この部品が $520$ g以上である確率を求めてください。

（解説）

平均と標準偏差の設定
平均が $500$ g、標準偏差が $20$ gです。

確率計算
重量が $520$ g以上の部品の確率を求めるには、正規分布の累積分布関数を使用します。まず、特定の重量を標準化します。

標準化
標準化の計算式は先ほどと同様です。

$Z = \frac{X - μ}{σ}$

ここで、 $X = 520$ 、 $μ = 500$ 、 $σ = 20$ なので、

$Z = \frac{520 - 500}{20} = 1$

累積分布関数を使用
標準正規分布の表または計算ツールを使用して、 $Z = 1$ に対応する値を見つけます。標準正規分布表によると、 $Z = 1$ に対応する値は約 $0.8413$ です。

確率の補完
$Z = 1$ 以下の確率が $0.8413$ なので、これより大きい部分の確率は $1$ から引いた値です

$P (X \geq 520) = 1 - 0.8413 = 0.1587$

結果の解釈
したがって、部品の重量が $520$ g以上である確率は約 $15.87$ %であることが分かります。

まとめ

正規分布は、多くの自然現象や社会現象を理解するための基本的なツールです。平均と標準偏差を使ってデータの分布を簡単に表現でき、広く応用されています。中心極限定理により、多くのデータの平均が正規分布に従うため、統計分析において非常に重要です。

さいごまで読んでいただきありがとうございました！

『統計の扉』で書いている記事

高校数学の解説
公務員試験の数学
統計学（統計検定2級レベル）

ぜひご覧ください！

数学でお困りの方は、コメントやXでご連絡ください。（Xはこちら）

私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。

”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。

URLをコピーしました！