等式を満たす点の位置
今回は空間ベクトルの問題です!
空間図形になると難しく感じるかもしれませんが、考え方は平面と同様ですし、適宜空間図形を切り取れば平面図形として見ることができます。例題と解説を用意してるので解いてみてください。
等式を満たす点の位置(問題)
四面体
>>詳細はこちらから
解説
この形を目指す
図を描く手順
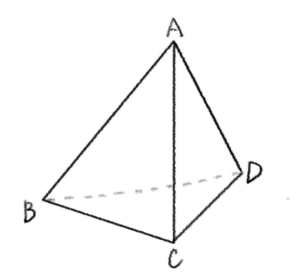
手順①
三角形
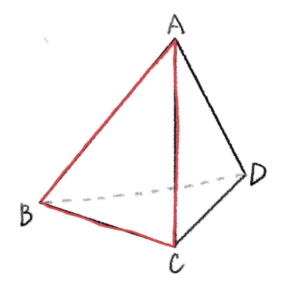
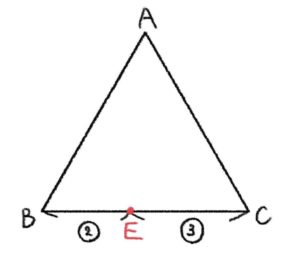
手順②
次に三角形
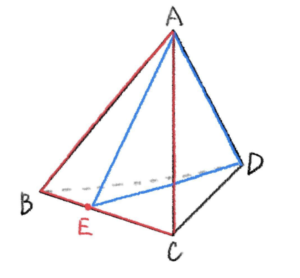
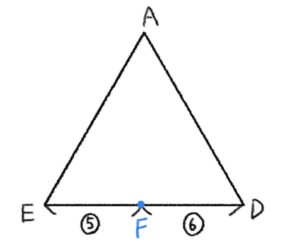
手順③
手順①, ② より導いた点
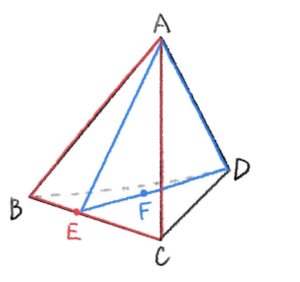
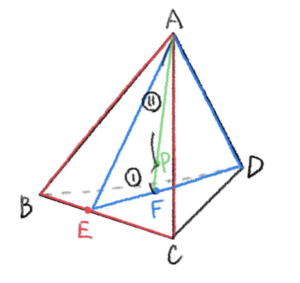
以上より、点
おわりに
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。



