【因数分解】ある文字について整理するタイプの因数分解

一つの文字について整理する因数分解

一般的な「 \(x^2+10x+21\) 」などの因数分解はできる方が多いのではないでしょうか？

答えは「 \((x+3)(x+7)\) 」となりますね。

積が \(21\) 、和が \(10\) になる組み合わせを探し、 \(3\) と \(7\) を導き出したわけです。

しかし、こう簡単に因数分解できないものも多数存在します。この記事では、 \(1\) つの文字について整理することで、因数分解できる問題を紹介します。

一つの文字について整理する因数分解（問題）

次の式を因数分解しなさい。

（\(1\)）\(x^3-x^2z-xy^2+y^2z\)
（\(2\)）\(2x^2-5xy-3y^2+3x+5y-2\)

答案の例

（\(1\)）　\(x^3-x^2z-xy^2+y^2z\)
　　　　\(=(-x^2+y^2)z+x(x^2-y^2)\)
　　　　\(=-(x^2-y^2)z+x(x^2-y^2)\)
　　　　\(=(x^2-y^2)(x-z)\)
　　　　\(=(x+y)(x-y)(x-z)\)

（\(2\)）　\(2x^2-5xy-3y^2+3x+5y-2\)
　　　　\(=2x^2-(5y-3)x-3y^2+5y-2\)
　　　　\(=2x^2-(5y-3)x-(y-1)(3y-2)\)
　　　　\(=\big\{x-(3y-2)\big\} \big\{2x+(y-1)\big\}\)
　　　　\(=(x-3y+2)(2x+y-1)\)

解説

（\(1\)）

今回の問題のように、複数の文字が入っている場合の因数分解では、何かの文字について整理するという思考が非常に役立ちます。

とりあえず、すべての文字について、降べきの順に並べてみる（次数の高い項から順に並べる）ことから始めてみましょう。

　\(x\) について　\(\longrightarrow x^3-x^2z-xy^2+y^2z\)
　\(y\) について　\(\longrightarrow (z-x)y^2+x^3-x^2z\)
　\(z\) について　\(\longrightarrow (-x^2+y^2)z+x^3-xy^2\)

\(x\) についてはすでに問題で整理されていたのでいいとして、\(y\) と \(z\) についての整理された式を見てみましょう。
こういった問題の基本形は、整理された後の式の定数項を見ると、まだ因数分解できます。

実際、\(y\) についての式では、\((z-x)y^2+x^2(x-z)\)
\(z\) についての式では、\((-x^2+y^2)z+x(x^2-y^2)\)
のように、共通因数でくくることができますね。

そうすると、前半の項と後半の項で、再び共通因数のように見える部分があります。
このように、少しずつ因数分解ができてくるわけです。

複数の文字が入った因数分解は、

①　ある文字について、降べきの順に並べる
②　定数項に当たる部分を因数分解してみる
③　その後、式全体を見て、再び因数分解できるかを考える

というステップで考えていく！

今回の解答例では、 \(z\) に関して整理して解いているので、 \(z\) について整理した式で考えていきます。

\(z\) についての式は、上記で紹介したように、\((-x^2+y^2)z+x(x^2-y^2)\) です。
また、手前の項について、マイナスでくくると、

　　\(-(x^2-y^2)z+x(x^2-y^2)\)
となりますね。こうすることで、 \(x^2-y^2\)を共通因数と見ることができるため、

　　　\((x^2-y^2)(x-z)\)
　　\(=(x+y)(x-y)(x-z)\)
と因数分解できます。

（\(2\)）

今回も先程と同様、ある文字について降べきの順に並べるところから始めていきます。
解答例では \(x\) について並べ替えているため、 \(x\) に焦点を絞ってまとめていきましょう。

　　　\(2x^2-5xy-3y^2+3x+5y-2\)
　　\(=2x^2-(5y-3)x-3y^2+5y-2\)

こうしてみると、定数項の部分が \(y\) に関する \(2\) 次方程式になっているので、因数分解できないか考えてみます。

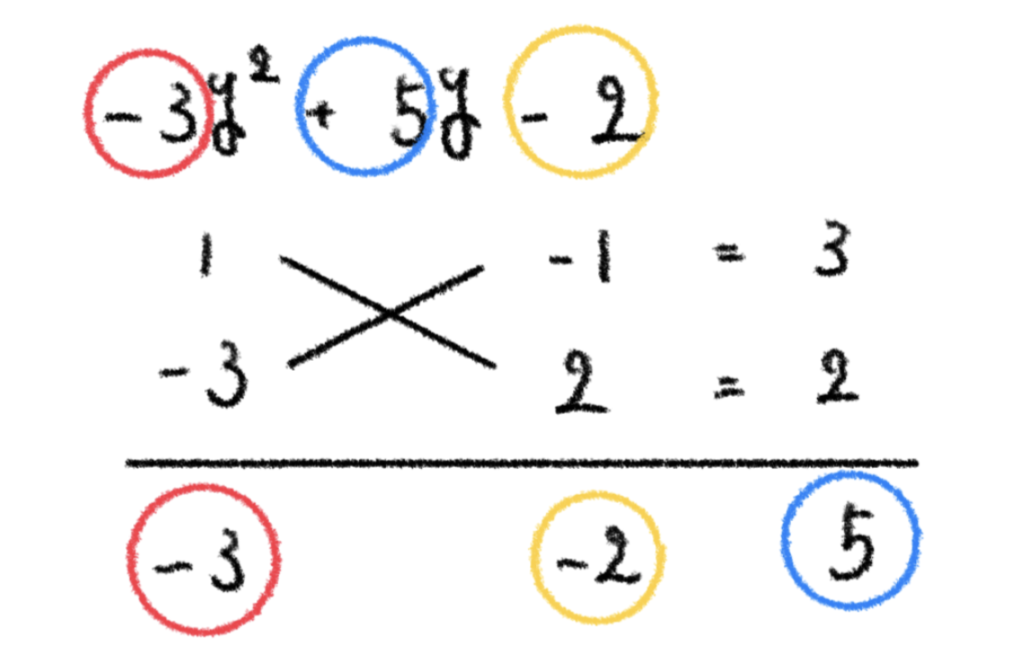
因数分解するためのたすき掛けを組むと上記のようになり、これにより、\((y-1)(-3y+2)\) となります。
※解答例とは少し違う形になっていますが、マイナスを \(3y-2\) に含まれば同じ結果となります。

ここで再度式を見て見ると、

\(2x^2-(5y-3)x-3y^2+5y-2\)
\(=2x^2-(5y-3)x+(y-1)(-3y+2)\)

これを \(x\) についての方程式と見なして、たすき掛けなどによる因数分解を試みてみます。

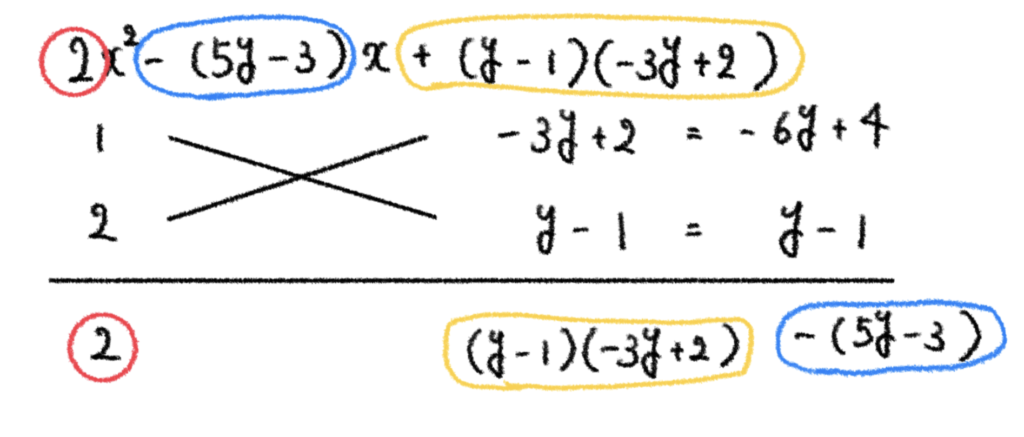
これによって、((x-3y+2)(2x+y-1))という結果を得ます。

こういった問題では、解き方が思いつきにくい以下のような並びになっているケースがあります。
　\(2x^2-3y^2-5xy+3x+5y-2\)

つまり、 \(x\) についてや \(y\) についてではなく、純粋に次数の高いものから降べきの順に並べている形です。
この中からある特定の文字についてのみ抜き出し、降べきの順に並べることが、こういった問題を攻略するポイントですね！

おわりに