今回は、三角形の角の大きさと辺の長さの関係について説明します。
三角形の形状を大雑把に分類すると次の3つに分けられます。
・鋭角三角形
・直角三角形
・鈍角三角形
上記の分類は、
(コサイン)
(コサイン)
という余弦(コサイン)の性質により分類することができます。
三角形の辺と角の大小関係
三角形について、次のことが成り立つことが知られています。
三角形の2辺の大小関係は、その向かい合う核の大小関係と一致する。
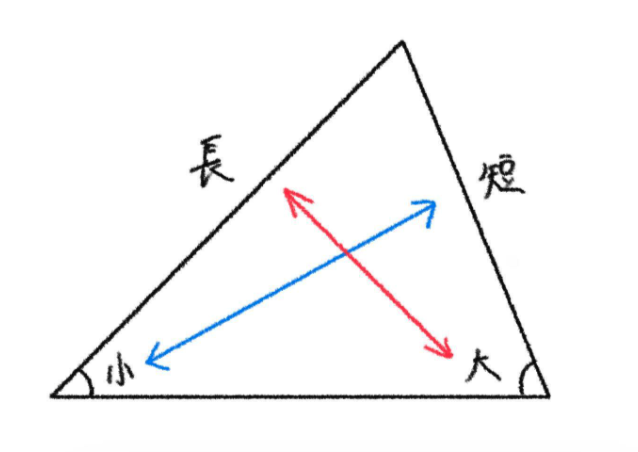
つまり、辺が大きければ大きいほど向かい合う角は大きくなるし、辺が小さければ小さいほど向かい合う角は小さくなる。
(証明)
次のような直線
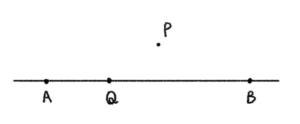
直線
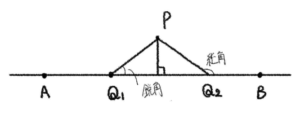
この結果から、点
まず、
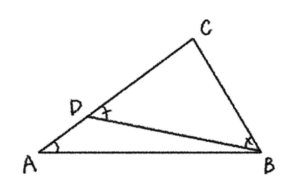
ここで、
>>詳細はこちらから
三角形の形状を調べる方法
直角三角形・鋭角三角形・鈍角三角形のいずれかであるかを調べる方法を説明します。
三角形の内角の和は
【三角形の形状を調べる方法】
三角形の内角の1つに着目したとき、その角が鋭角・直角・鈍角かを調べるには、その角のコサインの符号を調べれば良い。例えば、
の符号を調べれば良い。ここで、分母の
①
②
③
三角形の形状を調べる問題
問題
(1)
(2)
(3)
【(1) の解説】
最大辺の長さが
となるから、
よって、
【(2) の解説】
最大辺の長さが
となるから、
よって、
【(3) の解説】
最大辺の長さが
となるから、
よって、
おわりに
さいごまで読んでいただきありがとうございました!
『統計の扉』で書いている記事
- 高校数学の解説
- 公務員試験の数学
- 統計学(統計検定2級レベル)
ぜひご覧ください!
数学でお困りの方は、コメントやXでご連絡ください。(Xはこちら)
私自身、数学が得意になれたのはただ運が良かったんだと思っています。たまたま親が通塾させることに積極的だったり、友達が入るって理由でそろばんに入れたり、他の科目が壊滅的だったおかげで数学が(相対的に)得意だと勘違いできたり。
”たまたま”得意になれたこの恩を、今数学の学習に困っている人に還元できたらなと思っています。お金は取りません。できる限り(何百人から連絡が来たら難しいかもですが…)真摯に向き合おうと思っていますのでオアシスだと思ってご連絡ください。



