複素数の極形式と乗法、除法
極形式
これまで複素数と言えば、\(a+bi\) と表していたと思いますが、実は別の表し方があります！
それが、\(z=r(\cos\theta+i\sin\theta)\) です。\(r\) や \(\theta\) が与えられている場合は
ここからこの式について詳しく解説していきます。
複素数平面上で、\(0\) でない複素数 \(z=a+bi\) を表す点を \(P\) とする。\(OP=r\), 半直線 \(OP\) を動径と考えて、動径 \(OP\) の表す角を \(\theta\) とすると、
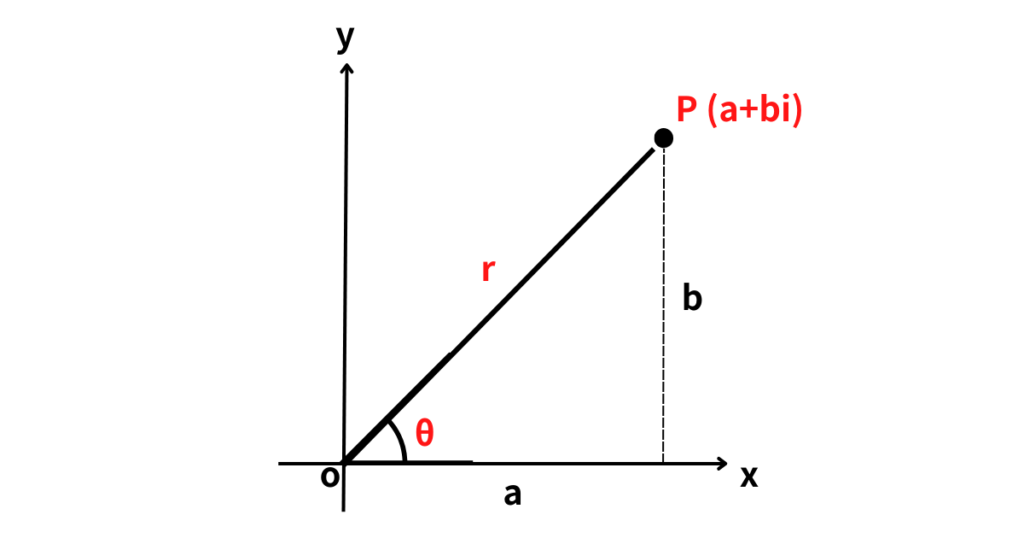
\(\alpha=r\cos\theta\), \(b=r\sin\theta\)
であるから、
\(z=r(\cos\theta+i\sin\theta)\) [\(r>0\)] \(\cdots\) ①
① を複素数 \(z\) の極形式という。このとき、\(r=|z|\) また、\(\theta\) を \(z\) の偏角といい \(\arg z\) で表す。特に、\(|z|=1\) のとき、
\(z=\cos\theta+i\sin\theta\)
複素数の乗法、除法
ここからは複素数同士の乗法（かけ算）、除法（割り算）について説明していきます！
\(z_1=r_1(\cos\theta_1+i\sin\theta_1)\),
\(z_2=r_2(\cos\theta_2+i\sin\theta_2)\) [\(r_1>0\), \(r_2>0\)]
とする。
① 複素数 \(z_1\), \(z_2\) の積の極形式
\(z_1z_2=r_1 r_2\{\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)\}\)
\(|z_1z_2|=|z_1||z_2|\), \(\arg(z_1z_2)=\arg z_1+\arg z_2\)
② 複素数 \(z_1\), \(z_2\) の商の極形式
\(\displaystyle\frac{z_1}{z_2}=\frac{r_1}{r_2}\{\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\}\)
\(\big|\displaystyle\frac{z_1}{z_2}\big|=\frac{|z_1|}{|z_2|}\), \(\arg\displaystyle\frac{z_1}{z_2}=\arg z_1-\arg z_2\) (\(z_2\neq 0\))
複素数の乗法と回転
複素数平面上で、\(P(z)\) とするとき、
点 \(r(\cos\theta+i\sin\theta)\cdot z\)
は、点 \(P\) を原点 \(O\) を中心として角 \(\theta\) だけ回転し、\(OP\) を \(r\) 倍に拡大（縮小）した点である。
複素数の極形式と乗法、除法（例題）
＞＞詳細はこちらから
（例題①）
次の複素数を極形式で表せ。ただし、偏角 \(\theta\) は \(0\leq \theta \leq 2\pi\) とする。
(1) \(-1+\sqrt{3}i\)
(2) \(-2i\)
（解説）
(1) \(-1+\sqrt{3}i\)
\(|-1+\sqrt{3}|=\sqrt{(-1)^2+(\sqrt{3})^2}=2\)
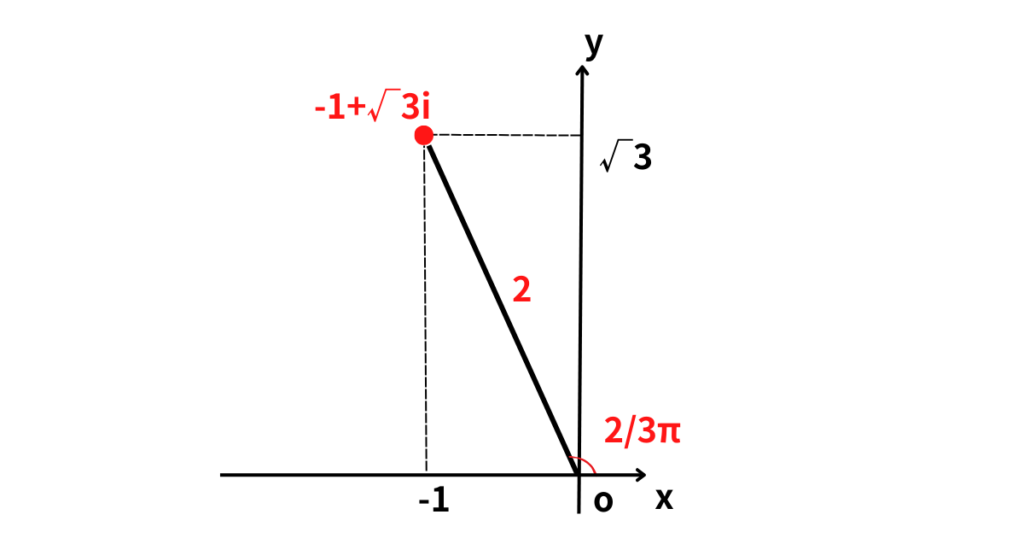
図より、\(\cos\theta=-\displaystyle\frac{1}{2}\), \(\sin\theta=\displaystyle\frac{\sqrt{3}}{2}\)
\(0\leq\theta<2\pi\) であるから \(\theta=\displaystyle\frac{2}{3}\pi\)
よって、
\(-1+\sqrt{3}i=2\big(\cos\displaystyle\frac{2}{3}\pi+i\sin\frac{2}{3}\pi\big)\)
(2) \(-2i\)
\(|-2i|=\sqrt{(-2)^2}=2\)
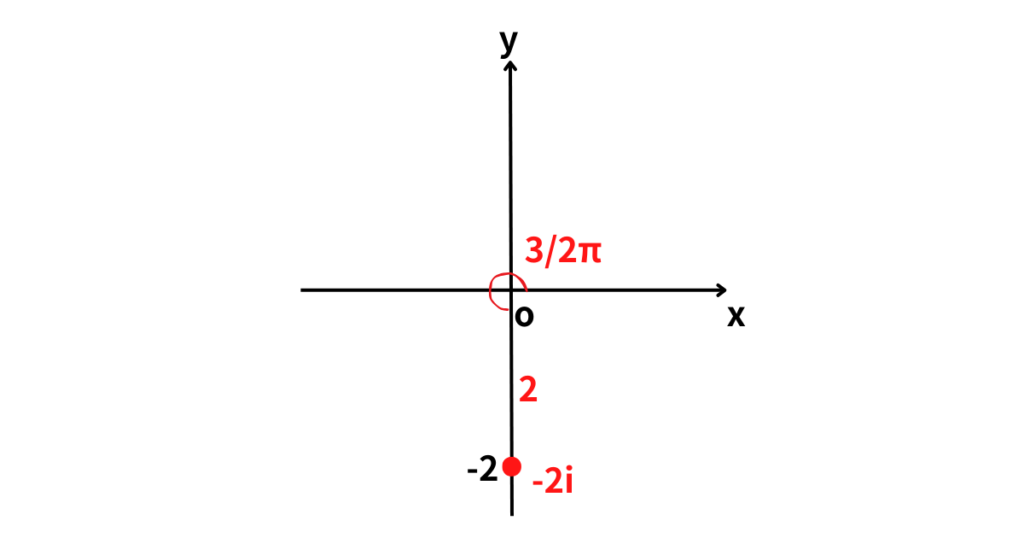
図より、\(\cos\theta=0\), \(\sin\theta=-1\)
\(0\leq\theta<2\pi\) であるから \(\theta=\displaystyle\frac{3}{2}\pi\)
よって、
\(-2i=2\big(\cos\displaystyle\frac{3}{2}\pi+i\sin\theta\frac{3}{2}\pi\big)\)
（例題②）
\(\alpha=2+2i\), \(\beta=1-\sqrt{3}i\) のとき、\(\alpha\beta\), \(\displaystyle\frac{\alpha}{\beta}\) をそれぞれ極形式で表せ。ただし、偏角 \(\theta\) は \(0\leq\theta<2\pi\) とする。
（解説）
\(\alpha=2\sqrt{2}\big(\displaystyle\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\big)\)
\(=2\sqrt{2}\big(\cos\displaystyle\frac{\pi}{4}+i\sin\frac{\pi}{4}\big)\)
\(\beta=2\big(\displaystyle\frac{1}{2}-\frac{\sqrt{3}}{2}i\big)\)
\(=2\big(\cos\displaystyle\frac{5}{3}\pi+i\sin\frac{5}{3}\pi\big)\)
よって、
\(\alpha\beta=2\sqrt{2}\cdot 2\big\{\cos\big(\displaystyle\frac{\pi}{4}+\frac{5}{3}\pi\big)+i\sin\big(\frac{\pi}{4}+\frac{5}{3}pi\big)\big\}\)
\(=4\sqrt{2}\big(\cos\displaystyle\frac{23}{12}\pi+i\sin\frac{23}{12}\pi\big)\)
\(\displaystyle\frac{\alpha}{\beta}=\frac{2\sqrt{2}}{2}\big\{\cos\big(\frac{\pi}{4}-\frac{5}{3}\pi\big)+i\sin\big(\frac{\pi}{4}-\frac{5}{3}\pi\big)\big\}\)
\(=\sqrt{2}\big\{\cos\big(-\displaystyle\frac{17}{12}\pi\big)+i\sin\big(-\frac{17}{12}\pi\big)\big\}\)
\(-\displaystyle\frac{17}{12}\pi=\frac{7}{12}\pi+2\pi\times (-1)\) から、
\(\displaystyle\frac{\alpha}{\beta}=\sqrt{2}\big(\cos\displaystyle\frac{7}{12}\pi+i\sin\frac{7}{12}\pi\big)\)
おわりに
さいごまで読んでいただきありがとうございました！
【最新】こちらの記事がおすすめ！