【確率】『独立試行とは？』解説と例題

独立試行の繰り返しを反復試行という。反復試行についての解説はこちらです！

例題

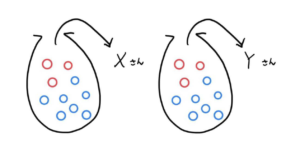
赤玉３個、青玉７個入った袋から、\(X\) さん,　\(Y\) さんがこの順番に１個の玉を取り出すとき、\(X\) さん,　\(Y\) さん がともに赤玉を引く確率を求める。

(1)　\(X\) さんが取り出した後、袋に戻して \(Y\) さんが取り出す。

(2)　\(X\) さんが取り出した後、袋に戻さずに \(Y\) さんが取り出す。

解説

\(X\) さんが１個の玉を取り出すという試行を \(S\)、
\(Y\) さんが１個の玉を取り出すという試行を \(T\) とする。

\(S\) では、赤玉を引くという事象 \(A\)
\(T\) では、赤玉を引くという事象 \(B\) が起こったとする。

(1)　\(X\) さんが取り出した後、袋に戻す場合

\(X\) さんが赤玉を取り出す確率は、\(\displaystyle\frac{3}{10}\)

\(X\) さんは袋に戻すので、袋の中の玉の数はリセットされます。

\(Y\) さんが赤玉を取り出す確率は、\(\displaystyle\frac{3}{10}\)

よって、\(\displaystyle\frac{3}{10}\times \displaystyle\frac{3}{10}=\displaystyle\frac{9}{100}\)

\(X\) さんが引く時と \(Y\) さんが引く時、互いに影響を及ぼしません。このとき、\(2\) つの試行 \(S\),　\(T\) は独立といいます。

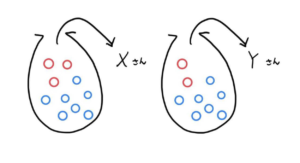
(2)　\(X\) さんが取り出した後、袋に戻さない場合

\(X\) さんが赤玉を取り出す確率は、\(\displaystyle\frac{3}{10}\)

\(X\) さんは袋に戻さないので、袋の中の玉の数は変化しています。

図

図のように、\(Y\) さんは、赤玉が一つ少ない状態の袋から赤玉を引きます。

\(Y\) さんが赤玉を取り出す確率は、\(\displaystyle\frac{2}{9}\)

よって、\(\displaystyle\frac{3}{10}\times \displaystyle\frac{2}{9}=\displaystyle\frac{6}{90}=\displaystyle\frac{1}{15}\)

\(X\) さんが引く時と \(Y\) さんが引く時、互いに影響を及ぼします。つまり、\(X\) さんが引いた玉によって、\(Y\) さんが赤玉を引けるかどうかの確率が変化します。このとき、\(2\) つの試行 \(S\),　\(T\) は独立ではないといいます。

（解説）

\(A\) が袋から \(1\) つ玉を取り出す試行と \(B\) が袋から \(1\) つ玉を取り出す試行はお互いに影響を及ぼし合いません。つまり、\(A\) が引いた玉によって \(B\) が袋から取り出す玉の種類が変わることはないので、この \(2\) つの試行は独立である。

\(A\) が勝つためには、同じ色が取り出される必要があります。そこで以下のように場合分けをして考えていきましょう。

[1]　\(A\),　\(B\) が白玉を取り出すとき

　\(A\) が白玉を取り出す：\(\frac{2}{5}\)
　\(B\) が白玉を取り出す：\(\frac{3}{5}\)

\(2\) つの試行は独立であることから、\(2\) つの確率は掛け算します。

よって、\(\displaystyle\frac{2}{5}\times\frac{3}{5}=\frac{6}{25}\)

[2]　\(A\),　\(B\) が黒玉を取り出すとき

　\(A\) が黒玉を取り出す：\(\frac{3}{5}\)
　\(B\) が黒玉を取り出す：\(\frac{2}{5}\)

\(2\) つの試行は独立であることから、\(2\) つの確率は掛け算します。

よって、\(\displaystyle\frac{2}{5}\times\frac{3}{5}=\frac{6}{25}\)

[1],　[2] は「または」で表されるので、

　\(\displaystyle\frac{6}{25}+\frac{6}{25}=\frac{12}{25}\)